|
P I P A
|
|
Sala 1
Pipas planas
|
Tópicos
 |
Retornando das férias, nada como iniciar os estudos se divertindo… |

I – Apresentação do Tema
  |
Pipa; papagaio; raia; quadrado; jamanta; arraia; barril; pandorga; maranhão… Não importa o nome; o brinquedo feito apenas com varetas de madeira, linha e papel fininho e colorido é sinônimo de alegria, magia, beleza, encantamento e muita diversão… |
  |
Até aqui, nenhuma novidade, não é?
Mas o que alguns talvez não saibam é que, ao longo da história, as pipas tiveram uma importância fundamental em muitas pesquisas e descobertas científicas. Que o digam
- Roger Bacon (1219-1292): filósofo inglês e monge franciscano;
- Leonardo da Vinci (1452-1519): artista, inventor e cientista italiano;
- Bartolomeu Lourenço de Gusmão (1685-1724); sacerdote, cientista e inventor luso-brasileiro;
- Benjamim Franklin (1706-1790): jornalista, editor, autor, filantropo, abolicionista, funcionário público, cientista, diplomata, inventor e enxadrista norte-americano;
- George Cayley (1777-1857): engenheiro e cientista inglês, considerado o fundador da aerodinâmica e o Pai da Aeronáutica;
entre outros.
Pois é, a pipa é muito mais do que um brinquedo…
Não acredita?
Mesmo os incrédulos já devem ter visto alguma figura mostrando um homem e uma pipa sendo empinada durante uma tempestade para provocar descargas elétricas, certo?
 |
 |
Pois bem, o homem retratado é, simplesmente, Benjamim Franklin: o inventor do para-raios. E olhem a pipa lá, ajudando em uma descoberta científica!
Até a toda poderosa Google anda utilizando balões e pipas para fornecer imagens para o banco do Google Earth.
A pipa é, de fato, um assunto repleto de surpresas para quem gosta de pesquisar e estudar; assim, a PIPA será o assunto central desta Sala de Atividades!
. . . E fiquem tranquilos, pois além dos tópicos de estudos teremos brincadeiras!
Mais uma figura que retrata Benjamim Franklin e suas pipas.
 Para obter informações sobre essa pintura, clique AQUI.
Para obter informações sobre essa pintura, clique AQUI.
II – Pequenas pesquisas para os membros dos Clubes
O que cada um de vocês sabe sobre as pipas?
Pesquisem os temas abaixo e, com certeza, vocês encontrarão muita coisa interessante sobre elas.
Busquem informações na Internet, em livros e não dispensem a ajuda imprescindível de seus professores.
1) História das pipas.
2) Diversos nomes da pipa no Brasil e no mundo.
3) Sucessos científicos com pipas.
4) Festivais de pipas pelo mundo.
5) Por que as pipas voam?
6) Cuidados ao soltar pipas.
7) Resistência dos diversos materiais utilizados na confecção de pipas.
III – Curiosidade: Modelos de pipas
Que tipos de pipa vocês conhecem?
Apresentamos abaixo alguns dos modelos mais conhecidos, observando que as nomenclaturas diferem, dependendo de cada região.

















Procurando por pipas diferentes?
Que tal estas:






Gostaram?
Visitem, então, esta página.
IV – A matemática das pipas diamante
Que objeto matemático é uma pipa diamante?
O próximo vídeo vai ajudar na resposta.
Pipas como formas geométricas
Vídeo disponibilizado pela Khan Academy
A partir das discussões feitas no vídeo, vamos registrar o que entenderemos matematicamente por uma pipa diamante.
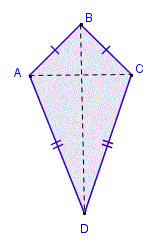
Nesta atividade, chamaremos de pipa diamante, ou simplesmente pipa, a todo quadrilátero que tenha dois pares de lados adjacentes congruentes.
Assim, uma pipa é um quadrilátero que tem dois pares de lados formados por segmentos consecutivos de mesmo comprimento.
No vídeo foram citadas três importantes formas geométricas: paralelogramo, losango e quadrado. Que tal vocês se reunirem para explorar a relação entre essas figuras e discutirem as questões que se seguem?
Questão 2.1:
Uma pipa é um paralelogramo? Um paralelogramo é uma pipa?
Justifiquem.
Questão 2.2:
Uma pipa é um losango? Um losango é uma pipa?
Justifiquem.
Questão 2.3:
Uma pipa é um quadrado? Um quadrado é uma pipa?
Justifiquem.
Questão 2.4:
Um losango é um quadrado? Um quadrado é um losango?
Justifiquem.
Questão 2.5:
Um paralelogramo é um losango? Um losango é um paralelogramo?
Justifiquem.
Questão 2.6:
Afinal, o que é um paralelogramo? E um losango? E um quadrado?
Questão 2.7:
As diagonais de um paralelogramo são perpendiculares entre si?
E as de um losango? E as de um quadrado? E as de uma pipa?
Justifiquem.
Questão 2.8:
As diagonais de um paralelogramo se dividem ao meio?
E as de um losango? E as de um quadrado? E as de uma pipa?
Justifiquem.
Para isso, abram o applet e movimentem os vértices do quadrilátero para obterem figuras distintas que os ajudarão em suas análises.
O applet poderá ser utilizado de duas maneiras:
- on-line – clicando no botão Applet, o aparato abrirá em outra janela do Navegador;
- off-line – clicando no botão Arquivo, vocês poderão copiar o arquivo .ggb e abri-lo no GeoGebra do computador ou tablet que estão utilizando. Se vocês não têm o GeoGebra instalado, basta visitar este site e procurar pela versão adequada ao dispositivo utilizado.
V – Explorando um pouco mais as pipas diamante
Já sabemos que uma pipa diamante/peixinho é um quadrilátero com dois pares de lados adjacentes congruentes; assim, sendo um quadrilátero, duas perguntas podem surgir:
Qual é a área de uma pipa diamante?
Para que serve essa área?
A área de uma pipa nos sugere, por exemplo, qual a quantidade de papel que precisamos para montá-la. Com o próximo vídeo vamos aprender uma maneira de calcular essa área.
Área de uma pipa
Vídeo disponibilizado pela Khan Academy
Simples e perfeito:
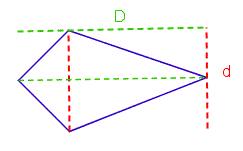 Se [tex]D[/tex] e [tex]d[/tex] são os comprimentos, respectivamente, da diagonal maior e da diagonal menor, então a área da pipa é dada por:
Se [tex]D[/tex] e [tex]d[/tex] são os comprimentos, respectivamente, da diagonal maior e da diagonal menor, então a área da pipa é dada por:
Área = [tex]\dfrac{D \times d}{2}[/tex]
Então, conhecendo os comprimentos das diagonais, que são os tamanhos das varetas que utilizamos para montar uma pipa diamante/peixinho, rapidamente conseguimos calcular a área: multiplicamos os dois comprimentos e, em seguida, dividimos o produto por 2.
Mas, e se não tivermos o comprimento das diagonais de uma pipa? A partir dos dois comprimentos dos seus lados será possível determinar sua área?
Reúnam os componentes de seus Clubes e tentem elucidar essa questão. O applet disponibilizado com certeza vai ajudar. Este applet também poderá ser utilizado on-line e off-line.
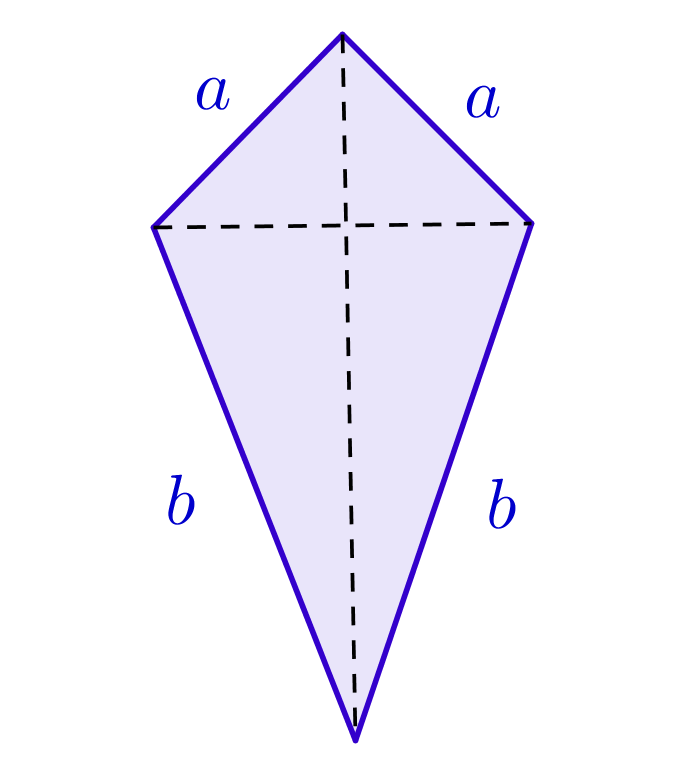
Questão 3.1:
Sejam a e b as medidas dos lados de uma pipa diamante.
É possível obter a área dessa pipa a partir dos valores a e b?
Justifiquem.
E já que vocês estão reunidos, que tal resolverem uma bela questão envolvendo pipas? Essa foi a questão 8 da Segunda Fase do Vestibular 2010 da UNICAMP e exige um pouco de conhecimento de trigonometria.

Vocês podem conferir a resposta dessa questão AQUI, ou AQUI.
VI – Oficina para construção de pipas planas
É sempre bom aprender!
E aprender se divertindo é melhor ainda!!!
Então, que tal vocês organizarem pequenas oficinas em suas escolas para construir pipas?
Nessas oficinas, enquanto pipas são construídas, conteúdos de geometria como o estudo de ângulos, área, perímetro, entre outros, podem ser discutidos pelos alunos, com a orientação de seus professores.
Vocês só precisarão providenciar:
- papel fininho;
- varetas;
- cola;
- linha;
- tesouras sem ponta;
- réguas;
- lápis e borrachas.
Abaixo disponibilizamos material para ajudá-los.
Ah, uma sugestão! Convidem os pais de vocês para participarem da oficina.
Com certeza eles terão muito para lhes ensinar!

Material de apoio
Clicando em cada link vocês terão acesso a uma página contendo instruções, vídeos, aparatos ou questionamentos para construção do respectivo tipo de pipa.
Agora, se vocês estiverem interessados em modelos diferentes de pipas, visitem ESTE SITE. Lá vocês vão encontrar muitos, mas muitos mesmo, modelos de pipas e seus respectivos esquemas de construção. O site não é em português, mas vocês entenderão, sem grandes dificuldades, os mais de 1600 esquemas disponibilizados.
ESTE é outro site que vocês podem visitar para encontrar planos de construção para modelos diferentes de pipa.

Vídeos e textos de apoio
Aqui estão alguns textos, sites e mais alguns vídeos para ajudá-los. Vejam se algum dos assuntos lhes interessa e cliquem no link correspondente.
✓ Como fazer os laços nas pontas das varetas.
✓ Como fazer uma pipa diamante/peixinho.
✓ Cuidados para que o papel não solte da armação de uma pipa durante o vôo.
✓ Os 10 Mandamentos do Pipeiro.
✓ Se a pipa não subir, aqui aparecem alguns possíveis defeitos.
Bons voos!
VII – Pipas no céu
Depois de um árduo, mas divertido trabalho, que tal vocês promoverem uma revoada de pipas? Parece uma ideia legal, não é?
A primeira coisa a fazer, antes de colocar as pipas no ar, é convidar um bombeiro ou um policial para fazer uma palestra sobre “Os 10 Mandamentos do pipeiro e outros cuidados necessários ao brincar de pipa”.
Depois, aproveitando a presença do bombeiro, ou do policial, reúnam-se com seus professores e organizem os passos iniciais do evento:
- Escolham o local.
- Decidam se vai acontecer apenas uma revoada de pipas ou um concurso de pipas.
- Definam a Comissão Organizadora do Evento.
Definida a Comissão, esta ficará responsável pela organização do Evento: datas, autorizações, convidados, divulgação, entre outros afazeres.
Se a opção for promover um concurso de pipas, será essencial providenciar um regulamento, definindo:
- Categorias, por exemplo:
– a pipa mais bonita;
– a pipa mais original;
– a maior pipa e a menor pipa;
– a pipa que voa mais alto.
- Tipos de participação, por exemplo:
– individual;
– por equipe;
– por sala de aula;
– por família.
- Regras
- Critérios de pontuação
- Premiação
- Jurados
- Inscrições (Poderá, por exemplo, ser arrecadado como inscrição um quilo de alimento não perecível, que poderá ser entregue a alguma instituição de caridade)
Para a escolha da data do evento, é prudente consultar o site do INMET – Instituto Nacional de Meteorologia.
Boa diversão!!!


➨ Uma proposta de ensino de geometria: Construindo Pipas (Último acesso em 20/06/20)
➨ A construção de pipas no ensino de matemática (Último acesso em 20/06/20)
➨ Soltar pipa dá aula de Educação Física, Geografia, Ciências e cidadania (Último acesso em 20/06/20)
Equipe COM – OBMEP
Junho de 2015.
➨ Coats Crafts Brasil (Último acesso em 20/06/20)
➨ Khan Academy (Último acesso em 20/06/20)
➨ Rafael pipas (Último acesso em 20/06/20)
➨ Silvio Voce, especialista em pipas (Último acesso em 20/08/18)
➨ www.culturamix.com (Último acesso em 20/06/20)
➨ YouTube (Último acesso em 20/20/06/20)