Ângulo Central e Ângulo Inscrito – Problemas

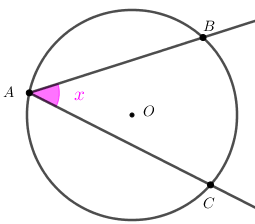
Problema 1: Na figura, o arco [tex]\stackrel{\textstyle\frown}{BC}[/tex] mede [tex]120^\circ.[/tex]
Calcule o valor de [tex]x.[/tex]

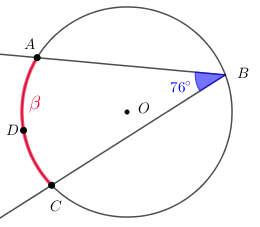
Problema 2: Na figura, o ângulo[tex]A\hat{B}C[/tex] mede [tex]76^\circ.[/tex]
Calcule a medida angular do arco [tex]\stackrel{\textstyle\frown}{\mathrm{ADC}}.[/tex]

Sabemos que a medida de um ângulo inscrito é a metade da medida do seu correspondente ângulo central e, consequentemente, a metade da medida angular do arco por eles definido.
Assim, se [tex]\beta[/tex] é a medida angular do arco [tex]\stackrel{\textstyle\frown}{\mathrm{ADC}}[/tex], então:

[tex]\qquad \beta=2\times 76^\circ=\fcolorbox{black}{#f6ebe1}{$152^\circ $} \, .[/tex]

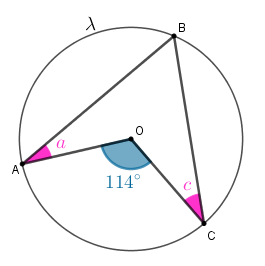
Problema 3: Na figura, [tex]A, \, B[/tex] e [tex]C[/tex] são pontos da circunferência [tex]\lambda[/tex] de centro em [tex]O[/tex] e [tex]a[/tex] e [tex]c[/tex] são as medidas dos ângulos com vértices em [tex]A[/tex] e [tex]C[/tex], respectivamente.
Determine, em graus, a soma [tex]a+c.[/tex]

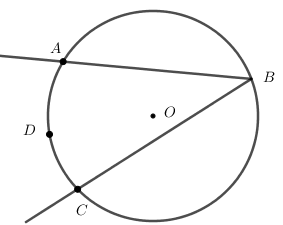
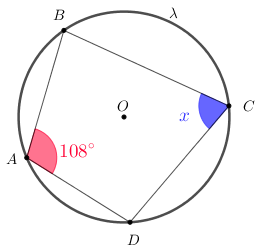
Problema 4: Na figura, [tex]A, \, B, \, C[/tex] e [tex]D[/tex] são pontos da circunferência [tex]\lambda[/tex] de centro em [tex]O[/tex].
Determine a medida [tex]x \, [/tex], em graus, indicada na figura.

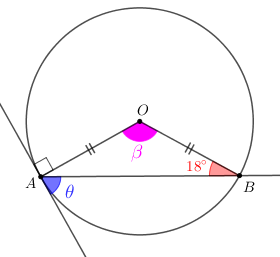
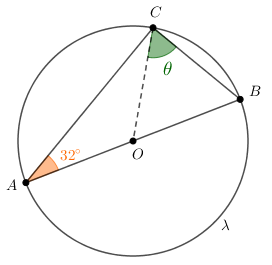
Problema 5: Na figura, [tex]A, \, B[/tex] e [tex]C[/tex] são pontos da circunferência [tex]\lambda[/tex] de centro em [tex]O[/tex].
Se [tex]\overline{AB}[/tex] é um diâmetro de [tex]\lambda \, [/tex], determine a medida [tex]\theta \, [/tex], em graus, indicada na figura.

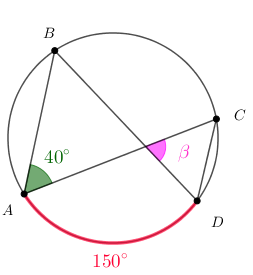
Problema 7: Determine a medida em graus [tex]\beta[/tex] indicada na figura abaixo.

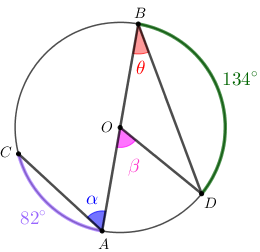
Problema 8: Na figura, [tex]A, \, B, \, C[/tex] e [tex]D[/tex] são pontos da circunferência de centro em [tex]O \, [/tex], sendo [tex]\overline{AB}[/tex] um diâmetro.
Conhecidas as medidas angulares dos arcos [tex]\stackrel{\textstyle\frown}{AC \, }[/tex] e [tex]\stackrel{\textstyle\frown}{BD \, }[/tex], conforme indicado na figura, determine, em graus, a soma [tex]\alpha+\beta+\theta.[/tex]

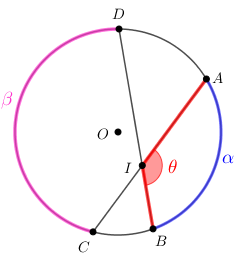
Desafio 1: Um ângulo excêntrico interior de uma circunferência é todo ângulo definido por duas cordas que se cruzam em um ponto interior da circunferência, diferente do centro.
Determinar a medida [tex]\theta[/tex] em graus do ângulo excêntrico interior [tex]A\hat{I}B[/tex] determinado pelas cordas [tex]\overline{AC}[/tex] e [tex]\overline{BD}[/tex] de uma circunferência de centro [tex]O \, [/tex], a partir das medidas angulares [tex]\alpha[/tex] e [tex]\beta[/tex] dos arcos [tex]\stackrel{\textstyle\frown}{AB \, }[/tex] e [tex]\stackrel{\textstyle\frown}{CD \, } \, [/tex], respectivamente, conforme indicado na figura abaixo.

Dicas:
(1) Lembre-se de que [tex]\alpha[/tex] e [tex]\beta[/tex] são as medidas em graus dos ângulos centrais [tex]A\hat{O}B[/tex] e [tex]C\hat{O}D[/tex] da circunferência de centro em [tex]O[/tex] que enxergam respectivamente os arcos [tex]\stackrel{\textstyle\frown}{AB \, }[/tex] e [tex]\stackrel{\textstyle\frown}{CD \, } \, .[/tex]
(2) O Teorema do ângulo externo pode ajudar.

Desafio 2: Um ângulo excêntrico exterior em uma circunferência é todo ângulo definido por duas semirretas que partem de um vértice exterior e que são secantes à circunferência.
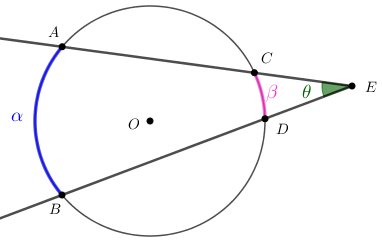
Sejam [tex]\overline{AC}[/tex] e [tex]\overline{BD}[/tex] duas cordas de uma circunferência de centro [tex]O[/tex] cujas retas suportes se intersectam em um ponto [tex]E[/tex] exterior à circunferência.
Determinar a medida [tex]\theta[/tex] em graus do ângulo excêntrico exterior [tex]A\hat{E}B[/tex], a partir das medidas angulares [tex]\alpha[/tex] e [tex]\beta[/tex] dos arcos [tex]\stackrel{\textstyle\frown}{AB \, }[/tex] e [tex]\stackrel{\textstyle\frown}{CD \, } \, [/tex], respectivamente, conforme indicado na figura abaixo.

Dicas:
(1) Lembre-se de que [tex]\alpha[/tex] e [tex]\beta[/tex] são as medidas em graus dos ângulos centrais [tex]A\hat{O}B[/tex] e [tex]C\hat{O}D[/tex] da circunferência de centro em [tex]O[/tex] que enxergam respectivamente os arcos [tex]\stackrel{\frown}{AB \, }[/tex] e [tex]\stackrel{\frown}{CD \, } \, .[/tex]
(2) O Teorema do ângulo externo pode ajudar.

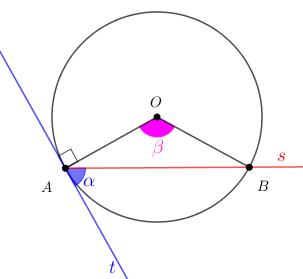
Desafio 3: Um ângulo de segmento em uma circunferência é todo ângulo cujo vértice é um ponto da circunferência, um dos lados é uma corda e o outro lado é tangente à circunferência no vértice do ângulo.
Determine a medida [tex]\alpha[/tex] do ângulo de segmento mostrado na figura abaixo, a partir da medida [tex]\beta[/tex] do ângulo central indicado.

Dicas:
(1) O triângulo [tex]ABO[/tex] é isósceles.
(2) Toda tangente a uma circunferência é perpendicular ao raio no ponto de tangência.

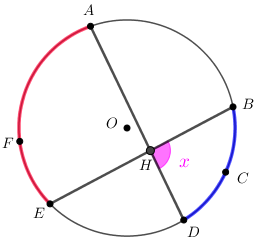
Problema 9: Na figura, o arco [tex]\stackrel{\textstyle\frown}{\mathrm{EFA}}[/tex] mede [tex]112^\circ[/tex] e o [tex]\stackrel{\textstyle\frown}{\mathrm{BCD}}[/tex] mede [tex]86^\circ.[/tex] Calcule o valor de [tex]x.[/tex]

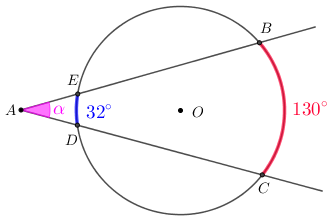
Problema 10: Na figura, o arco [tex]\stackrel{\textstyle\frown}{\mathrm{BC}}[/tex] mede [tex]130^\circ[/tex] e o [tex]\stackrel{\textstyle\frown}{\mathrm{DE}}[/tex] mede [tex]32^\circ.[/tex] Qual o valor de [tex]\alpha \, [/tex]?

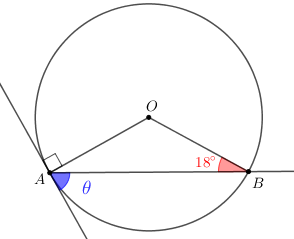
Problema 11: Determine a medida [tex]\theta[/tex] indicada na figura abaixo.

Observe que o triângulo [tex]OAB[/tex] é isósceles, já que os segmentos [tex]\overline{OA}[/tex] e [tex]\overline{OB}[/tex] são raios da circunferência; assim os ângulos da base desse triângulo são congruentes.
Como a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ [/tex], segue que:
[tex]\qquad \, \beta+18^\circ + 18^\circ=180^\circ[/tex]
[tex]\qquad \, \beta+36^\circ=180^\circ[/tex]
[tex]\qquad \, \beta=180^\circ-36^\circ[/tex]
[tex]\qquad \, \beta=144^\circ \, .[/tex]

Perceba, agora, que o ângulo de medida [tex]\theta[/tex] mostrado na figura é um ângulo de segmento, então, pelo Desafio 3, segue que:
[tex]\qquad \, \theta=\dfrac{\beta}{2}[/tex]

[tex]\qquad \, \theta=\dfrac{144^\circ}{2}[/tex]

[tex]\qquad \, \fcolorbox{black}{#eee0e5}{$\theta=72^\circ$} \, .[/tex]