Clique no botão abaixo para visualizar a Sala.
Um passeio pelo mundo da Equação Quadrática
Problemas envolvendo equações do 2º Grau
Problema 1:
Em quantos triângulos retângulos as medidas dos lados são números inteiros consecutivos?
Justifique.
Em quantos triângulos retângulos as medidas dos lados são números inteiros consecutivos?
Justifique.
Em apenas um.
Problema 2:
O supermercado que fica próximo à minha casa vai aumentar [tex]x[/tex] metros no comprimento e [tex]x[/tex] metros na largura do atual estacionamento, de modo que o estacionamento novo tenha, mais ou menos, [tex]400\text{ m}^2.[/tex] Determinar [tex]x[/tex].
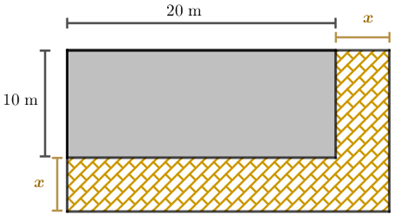
O supermercado que fica próximo à minha casa vai aumentar [tex]x[/tex] metros no comprimento e [tex]x[/tex] metros na largura do atual estacionamento, de modo que o estacionamento novo tenha, mais ou menos, [tex]400\text{ m}^2.[/tex] Determinar [tex]x[/tex].

Você pode conferir a sua resposta a partir deste applet. É só movimentar horizontalmente o ponto P para obter a área de, aproximadamente, [tex]400\text{ m}^2[/tex] para o novo estacionamento e observar o valor de [tex]x[/tex] correspondente.
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para movimentar o ponto P clique sobre ele com qualquer botão do mouse, mantenha o mouse pressionado e faça o movimento. (Se você estiver utilizando um celular ou um tablet, basta tocar levemente no ponto e fazer o movimento.)
(3) Se você estiver usando um computador, você também poderá fazer o movimento do ponto com o seu teclado. Para isso, clique no ponto com o botão esquerdo do mouse e faça os movimentos com as teclas “mover para direita” ou “mover para esquerda”. (Para movimentos “mais finos”, mantenha a tecla Shift do teclado apertada enquanto você faz o movimento.)
(4) Se quiser voltar para a visualização inicial, clique nas setinhas circulares que aparecem no canto superior direito da janela do aplicativo.
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para movimentar o ponto P clique sobre ele com qualquer botão do mouse, mantenha o mouse pressionado e faça o movimento. (Se você estiver utilizando um celular ou um tablet, basta tocar levemente no ponto e fazer o movimento.)
(3) Se você estiver usando um computador, você também poderá fazer o movimento do ponto com o seu teclado. Para isso, clique no ponto com o botão esquerdo do mouse e faça os movimentos com as teclas “mover para direita” ou “mover para esquerda”. (Para movimentos “mais finos”, mantenha a tecla Shift do teclado apertada enquanto você faz o movimento.)
(4) Se quiser voltar para a visualização inicial, clique nas setinhas circulares que aparecem no canto superior direito da janela do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
Observações: O GeoGebra trabalha com arredondamentos. A visualização de várias situações particulares de um fato matemático não substitui sua demonstração.
Problema 3:
Determine o valor de [tex]x[/tex] de modo que a área do polígono da Figura 1 seja igual à área do polígono da Figura 2.
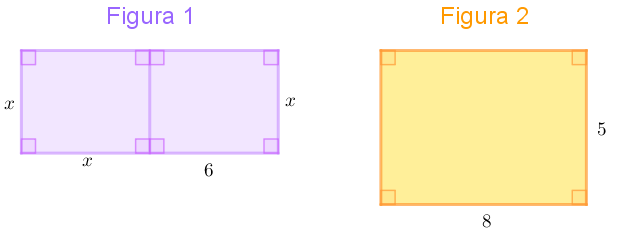
Determine o valor de [tex]x[/tex] de modo que a área do polígono da Figura 1 seja igual à área do polígono da Figura 2.

4 unidades de comprimento.
Problema 4:
Você viu na Sala 1 o procedimento realizado por al-Khwarizmi para solucionar a equação [tex]x^2+10x=39[/tex]. Essa equação resulta da formulação do seguinte problema :
“Qual o quadrado que somado a [tex]10[/tex] raízes dá o número [tex]39[/tex]?”
Já que esse problema pode ter sido resolvido geometricamente, tente acompanhar e entender a solução geométrica do problema apresentada abaixo.
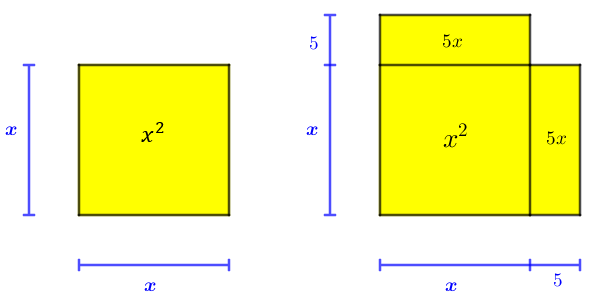
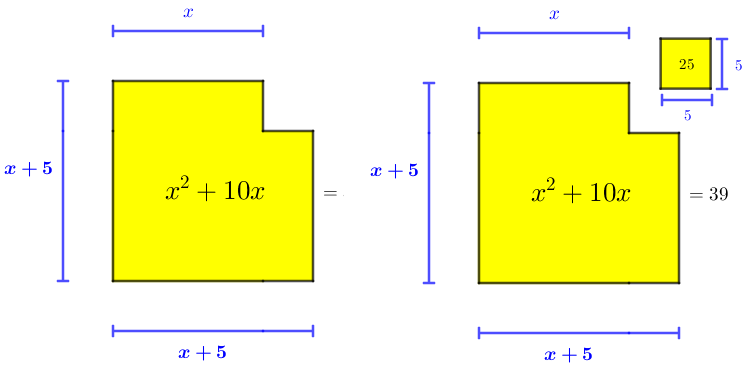
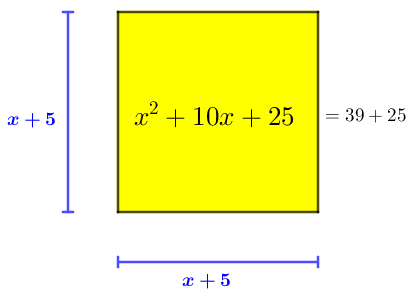
Você viu na Sala 1 o procedimento realizado por al-Khwarizmi para solucionar a equação [tex]x^2+10x=39[/tex]. Essa equação resulta da formulação do seguinte problema :
“Qual o quadrado que somado a [tex]10[/tex] raízes dá o número [tex]39[/tex]?”
Já que esse problema pode ter sido resolvido geometricamente, tente acompanhar e entender a solução geométrica do problema apresentada abaixo.



Problema 5:
Sabendo que a área da figura abaixo tem [tex]65\text{ cm}^2[/tex], determine o valor de [tex]x.[/tex]
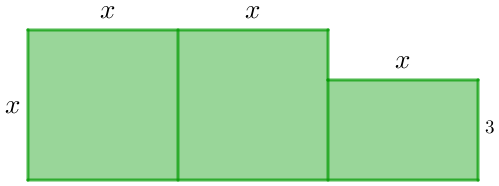
Sabendo que a área da figura abaixo tem [tex]65\text{ cm}^2[/tex], determine o valor de [tex]x.[/tex]

[tex]x=5\text{ cm}[/tex].
Problema 6:
É possível utilizar a técnica de completamento de quadrado para encontrar as raízes de uma equação quadrática e esse processo pode ser visualizado geometricamente.
As figuras abaixo ilustram o completamento de quadrado que pode ser feito para determinar as raízes da equação [tex]x^2+4x-21=0[/tex].
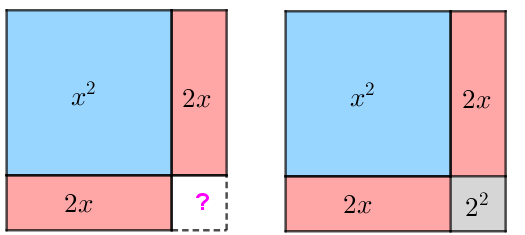
Interprete algebricamente o completamento de quadrado ilustrado por essas figuras e resolva a equação em questão.
É possível utilizar a técnica de completamento de quadrado para encontrar as raízes de uma equação quadrática e esse processo pode ser visualizado geometricamente.
As figuras abaixo ilustram o completamento de quadrado que pode ser feito para determinar as raízes da equação [tex]x^2+4x-21=0[/tex].

Interprete algebricamente o completamento de quadrado ilustrado por essas figuras e resolva a equação em questão.
Problema 7:
Utilize os polígonos que aparecem na figura abaixo e resolva a equação [tex]x^2+12x-13=0[/tex] utilizando o processo de completamento de quadrado.
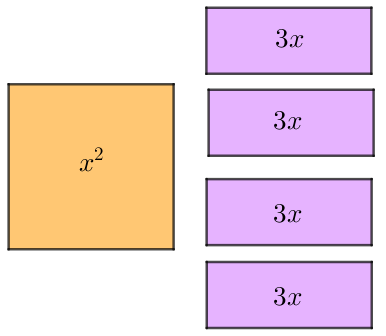
Utilize os polígonos que aparecem na figura abaixo e resolva a equação [tex]x^2+12x-13=0[/tex] utilizando o processo de completamento de quadrado.

Problema 8:
Seu Márcio quer aproveitar um rolo de tela com [tex]32[/tex] metros de comprimento para fazer um cercado novo na sua chácara e aumentar a sua horta.
Para que a nova horta tenha uma área retangular com, mais ou menos, [tex]60\text{ m}^2[/tex], quais devem ser as dimensões do terreno retangular que será cercado?
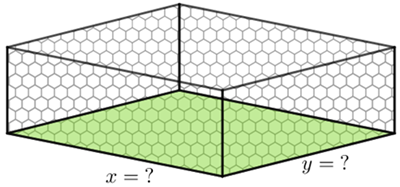
Seu Márcio quer aproveitar um rolo de tela com [tex]32[/tex] metros de comprimento para fazer um cercado novo na sua chácara e aumentar a sua horta.
Para que a nova horta tenha uma área retangular com, mais ou menos, [tex]60\text{ m}^2[/tex], quais devem ser as dimensões do terreno retangular que será cercado?

É um terreno retangular de [tex]6\text{ m}\times 10\text{ m}[/tex].
Problema 9:
O triângulo que aparece na figura abaixo tem área igual a [tex]20\text{ m}^2[/tex]. Determinar a medida da sua altura.
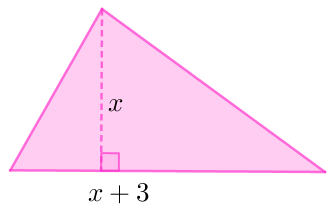
O triângulo que aparece na figura abaixo tem área igual a [tex]20\text{ m}^2[/tex]. Determinar a medida da sua altura.

[tex]x=5\text{ m}[/tex].
Problema 10:
Comprei algumas garrafas de vinho por 540 reais.
Como obtive um desconto de 15 reais no preço de cada garrafa, consegui comprar três garrafas a mais do que eu previ comprar inicialmente.
Quantas garrafas de vinho eu comprei?
Comprei algumas garrafas de vinho por 540 reais.
Como obtive um desconto de 15 reais no preço de cada garrafa, consegui comprar três garrafas a mais do que eu previ comprar inicialmente.
Quantas garrafas de vinho eu comprei?
12 garrafas.
Problema 11:
De um quadrado de lados com comprimento [tex]16\text{ cm}[/tex], retiramos a partir de cada vértice um quadradinho de lados medindo [tex]x\text{ cm}[/tex].
Se a área da figura final é [tex]220\text{ cm}^2[/tex], qual o comprimento dos lados dos quatro quadradinhos retirados?
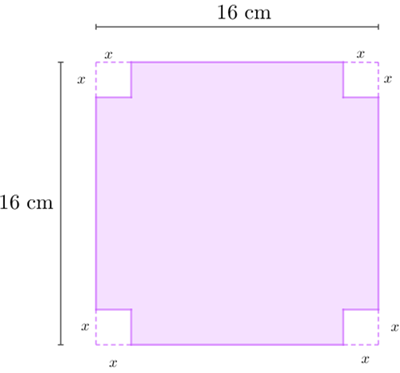
De um quadrado de lados com comprimento [tex]16\text{ cm}[/tex], retiramos a partir de cada vértice um quadradinho de lados medindo [tex]x\text{ cm}[/tex].
Se a área da figura final é [tex]220\text{ cm}^2[/tex], qual o comprimento dos lados dos quatro quadradinhos retirados?

Você pode conferir a sua resposta com este applet. É só movimentar horizontalmente o ponto colorido de preto que aparece na tela do aplicativo para obter a área de, aproximadamente, [tex]220\text{ cm}^2[/tex] para a figura final e observar o valor de [tex]x[/tex] correspondente.
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para movimentar o ponto colorido de preto clique sobre ele com qualquer botão do mouse, mantenha o mouse pressionado e faça o movimento. (Se você estiver utilizando um celular ou um tablet, basta tocar levemente no ponto e fazer o movimento.)
(3) Se você estiver usando um computador, você também poderá fazer o movimento do ponto com o seu teclado. Para isso, clique no ponto com o botão esquerdo do mouse e faça os movimentos com as teclas “mover para direita” ou “mover para esquerda”. (Para movimentos “mais finos”, mantenha a tecla Shift do teclado apertada enquanto você faz o movimento.)
(4) Se quiser voltar para a visualização inicial, clique nas setinhas circulares que aparecem no canto superior direito da janela do aplicativo.
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para movimentar o ponto colorido de preto clique sobre ele com qualquer botão do mouse, mantenha o mouse pressionado e faça o movimento. (Se você estiver utilizando um celular ou um tablet, basta tocar levemente no ponto e fazer o movimento.)
(3) Se você estiver usando um computador, você também poderá fazer o movimento do ponto com o seu teclado. Para isso, clique no ponto com o botão esquerdo do mouse e faça os movimentos com as teclas “mover para direita” ou “mover para esquerda”. (Para movimentos “mais finos”, mantenha a tecla Shift do teclado apertada enquanto você faz o movimento.)
(4) Se quiser voltar para a visualização inicial, clique nas setinhas circulares que aparecem no canto superior direito da janela do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
Observações: O GeoGebra trabalha com arredondamentos. A visualização de várias situações particulares de um fato matemático não substitui sua demonstração.
Problema 12:
A figura abaixo tem área igual a [tex]100\text{ cm}^2[/tex] e perímetro [tex]44\text{ cm}.[/tex] Determinar [tex]x~[/tex] e [tex]~y.[/tex]
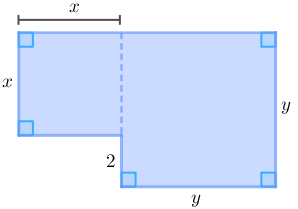
A figura abaixo tem área igual a [tex]100\text{ cm}^2[/tex] e perímetro [tex]44\text{ cm}.[/tex] Determinar [tex]x~[/tex] e [tex]~y.[/tex]

[tex]x=6\text{ cm}~[/tex] e [tex]~y=8\text{ cm}[/tex].
Problema 13:
Na figura abaixo, a área amarela mede [tex]63\text{ cm}^2[/tex] e a diferença entre [tex]x~[/tex] e [tex]~y~[/tex] é [tex]5.[/tex]
Calcule a área do triângulo alaranjado.
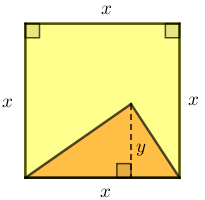
Na figura abaixo, a área amarela mede [tex]63\text{ cm}^2[/tex] e a diferença entre [tex]x~[/tex] e [tex]~y~[/tex] é [tex]5.[/tex]
Calcule a área do triângulo alaranjado.

[tex]18\text{ cm}^2[/tex].
Problema 14:
Na figura abaixo, vemos dois quadrados e dois retângulos.
Sabendo que a área total da figura mede [tex]100\text{ dm}^2[/tex], determine a área de cada polígono que a compõe.
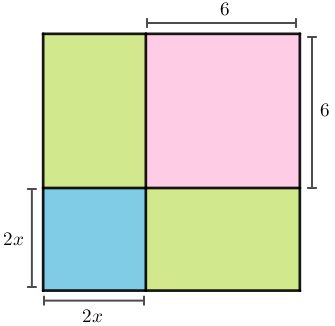
Na figura abaixo, vemos dois quadrados e dois retângulos.
Sabendo que a área total da figura mede [tex]100\text{ dm}^2[/tex], determine a área de cada polígono que a compõe.

Quadrado rosa: [tex]36\text{ dm}^2[/tex].
Quadrado azul: [tex]16\text{ dm}^2[/tex].
Cada retângulo: [tex]24\text{ dm}^2[/tex].
Quadrado azul: [tex]16\text{ dm}^2[/tex].
Cada retângulo: [tex]24\text{ dm}^2[/tex].
Problema 15:
(PUC – SP) Uma bola é largada do alto de um edifício e cai em direção ao solo. Sua altura [tex]h[/tex] em relação ao solo, [tex]t[/tex] segundos após o lançamento, é dada pela expressão [tex]h = −25t^2 + 625.[/tex]
Após quantos segundos do lançamento a bola atingirá o solo?
(PUC – SP) Uma bola é largada do alto de um edifício e cai em direção ao solo. Sua altura [tex]h[/tex] em relação ao solo, [tex]t[/tex] segundos após o lançamento, é dada pela expressão [tex]h = −25t^2 + 625.[/tex]
Após quantos segundos do lançamento a bola atingirá o solo?
[tex]5[/tex] segundos.
Problema 16:
O retângulo e o trapézio que aparecem na figura abaixo têm a mesma medida de área.
Que medida é essa?
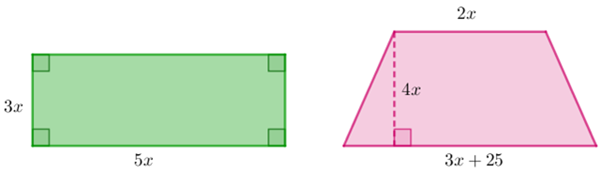
O retângulo e o trapézio que aparecem na figura abaixo têm a mesma medida de área.
Que medida é essa?

[tex]1\,500[/tex] unidades de área.
Problema 17:
Determine o valor de [tex]k[/tex] pra que a equação [tex]\boxed{\left(k^2-4\right)x^3 +\left(k-2\right)x^2+7x-8=0}[/tex] seja uma equação quadrática.
Determine o valor de [tex]k[/tex] pra que a equação [tex]\boxed{\left(k^2-4\right)x^3 +\left(k-2\right)x^2+7x-8=0}[/tex] seja uma equação quadrática.
[tex]k=-2[/tex].
Problema 18:
(ENEM 2013 – Adaptado) A temperatura [tex]T[/tex] de um forno (em graus centígrados) é reduzida por um sistema a partir do instante de seu desligamento ([tex]t = 0[/tex]) e varia de acordo com a expressão [tex]T=−\dfrac{t^2}{4}+400[/tex], com [tex]t[/tex] em minutos. Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge a temperatura de [tex]39^\circ C[/tex].
Qual o tempo mínimo de espera, em minutos, após se desligar o forno, para que a porta possa ser aberta?
(ENEM 2013 – Adaptado) A temperatura [tex]T[/tex] de um forno (em graus centígrados) é reduzida por um sistema a partir do instante de seu desligamento ([tex]t = 0[/tex]) e varia de acordo com a expressão [tex]T=−\dfrac{t^2}{4}+400[/tex], com [tex]t[/tex] em minutos. Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge a temperatura de [tex]39^\circ C[/tex].
Qual o tempo mínimo de espera, em minutos, após se desligar o forno, para que a porta possa ser aberta?
[tex]t=38[/tex].
Problema 19:
(ENEM 2016 – Adaptado) Para evitar uma epidemia, a Secretaria de Saúde de uma cidade dedetizou todos os bairros, de modo a evitar a proliferação do mosquito da dengue. Sabe-se que o número [tex]f[/tex] de infectados é dado pela expressão [tex]f= − 2t^2 + 120t[/tex] (em que [tex]t[/tex] é expresso em dia e [tex]t = 0[/tex] é o dia anterior à primeira infecção) e que tal expressão é válida para os [tex]60[/tex] primeiros dias da epidemia.
A Secretaria de Saúde decidiu que uma segunda dedetização deveria ser feita no dia em que o número de infectados chegasse à marca de [tex]1600[/tex] pessoas, e uma segunda dedetização precisou acontecer.
A segunda dedetização começou no:
A) 19º dia.
B) 20º dia.
C) 29º dia.
D) 30º dia.
E) 60º dia.
(ENEM 2016 – Adaptado) Para evitar uma epidemia, a Secretaria de Saúde de uma cidade dedetizou todos os bairros, de modo a evitar a proliferação do mosquito da dengue. Sabe-se que o número [tex]f[/tex] de infectados é dado pela expressão [tex]f= − 2t^2 + 120t[/tex] (em que [tex]t[/tex] é expresso em dia e [tex]t = 0[/tex] é o dia anterior à primeira infecção) e que tal expressão é válida para os [tex]60[/tex] primeiros dias da epidemia.
A Secretaria de Saúde decidiu que uma segunda dedetização deveria ser feita no dia em que o número de infectados chegasse à marca de [tex]1600[/tex] pessoas, e uma segunda dedetização precisou acontecer.
A segunda dedetização começou no:
A) 19º dia.
B) 20º dia.
C) 29º dia.
D) 30º dia.
E) 60º dia.
Alternativa B.
Problema 20:
(ENEM 2021 – Segunda aplicação) Um diretor esportivo organiza um campeonato no qual haverá disputa de times em turno e returno, isto é, cada time jogará duas vezes com todos os outros, totalizando [tex]380[/tex] partidas a serem disputadas.
A quantidade de times ([tex]x[/tex]) que faz parte desse campeonato pode ser calculada pela equação:
A) [tex]x = 380-x^2 [/tex]
B) [tex] x^2-x=380[/tex]
C) [tex]x^2=380[/tex]
D) [tex]2x-x=380[/tex]
E) [tex]2x=380[/tex]
(ENEM 2021 – Segunda aplicação) Um diretor esportivo organiza um campeonato no qual haverá disputa de times em turno e returno, isto é, cada time jogará duas vezes com todos os outros, totalizando [tex]380[/tex] partidas a serem disputadas.
A quantidade de times ([tex]x[/tex]) que faz parte desse campeonato pode ser calculada pela equação:
A) [tex]x = 380-x^2 [/tex]
B) [tex] x^2-x=380[/tex]
C) [tex]x^2=380[/tex]
D) [tex]2x-x=380[/tex]
E) [tex]2x=380[/tex]
Alternativa B.
Problema 21:
(UFPR, 2010 – 1ª Fase) A soma das áreas dos três quadrados que aparecem na figura é igual a [tex]83 \text{ cm}^2[/tex].
Calcule a área do quadrado maior.
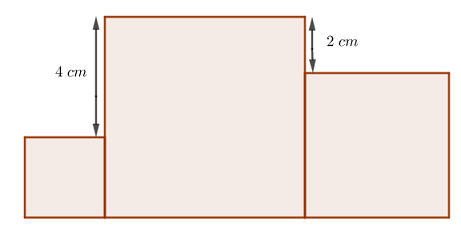
(UFPR, 2010 – 1ª Fase) A soma das áreas dos três quadrados que aparecem na figura é igual a [tex]83 \text{ cm}^2[/tex].
Calcule a área do quadrado maior.

Mais do que a resposta, confira a solução AQUI.
Problema 22:
(IME-2014/2015 – 2º Fase) Encontre as soluções reais da equação:
[tex]\quad \quad \sqrt{x+\sqrt{4x-4}}+\sqrt{x-\sqrt{4x-4}}=\sqrt{x+3}\,.[/tex]
(IME-2014/2015 – 2º Fase) Encontre as soluções reais da equação:
[tex]\quad \quad \sqrt{x+\sqrt{4x-4}}+\sqrt{x-\sqrt{4x-4}}=\sqrt{x+3}\,.[/tex]
Mais do que a resposta, confira a solução AQUI.
Problema 23:
Um comerciante possui uma loja e um depósito de materiais de construção.
O formato dos terrenos onde a loja e o depósito estão construídos é quadrado e juntos os dois terrenos ocupam uma área de [tex]596\, m^2[/tex]. O lado de um dos terrenos tem [tex] 6\, m[/tex] a mais que o do outro terreno.
Quais os comprimentos dos lados de cada terreno?
Um comerciante possui uma loja e um depósito de materiais de construção.
O formato dos terrenos onde a loja e o depósito estão construídos é quadrado e juntos os dois terrenos ocupam uma área de [tex]596\, m^2[/tex]. O lado de um dos terrenos tem [tex] 6\, m[/tex] a mais que o do outro terreno.
Quais os comprimentos dos lados de cada terreno?
Mais do que a resposta, confira a solução AQUI.
Problema 24:
Um pai deixou para seus filhos uma herança de [tex] R$ \hspace{0.1cm} 1,2[/tex] milhão. Três dos filhos renunciaram suas partes e, com isso, os demais receberam um adicional de [tex] R$ \hspace{0.1cm}90 [/tex] mil.
Determine quantos filhos tinha esse pai.
Um pai deixou para seus filhos uma herança de [tex] R$ \hspace{0.1cm} 1,2[/tex] milhão. Três dos filhos renunciaram suas partes e, com isso, os demais receberam um adicional de [tex] R$ \hspace{0.1cm}90 [/tex] mil.
Determine quantos filhos tinha esse pai.
Mais do que a resposta, confira a solução AQUI.
Problema 25:
(ENEM– Adaptado) Uma padaria vende, em média, [tex]100[/tex] pães especiais por dia e arrecada com essas vendas, em média, [tex]R\$\ 300,00[/tex]. Constatou-se que a quantidade de pães especiais vendidos diariamente aumenta, caso o preço seja reduzido, de acordo com a equação [tex]\boxed{q=400–100p}[/tex], na qual [tex]q[/tex] representa a quantidade de pães especiais vendidos diariamente e [tex]p[/tex], o seu preço em reais.
A fim de aumentar o fluxo de clientes, o gerente da padaria decidiu fazer uma promoção. Para tanto, modificará o preço do pão especial de modo que a quantidade a ser vendida diariamente seja a maior possível, sem diminuir a média de arrecadação diária na venda desse produto.
Qual deve ser o preço [tex]p[/tex], em reais, do pão especial nessa promoção?
(ENEM– Adaptado) Uma padaria vende, em média, [tex]100[/tex] pães especiais por dia e arrecada com essas vendas, em média, [tex]R\$\ 300,00[/tex]. Constatou-se que a quantidade de pães especiais vendidos diariamente aumenta, caso o preço seja reduzido, de acordo com a equação [tex]\boxed{q=400–100p}[/tex], na qual [tex]q[/tex] representa a quantidade de pães especiais vendidos diariamente e [tex]p[/tex], o seu preço em reais.
A fim de aumentar o fluxo de clientes, o gerente da padaria decidiu fazer uma promoção. Para tanto, modificará o preço do pão especial de modo que a quantidade a ser vendida diariamente seja a maior possível, sem diminuir a média de arrecadação diária na venda desse produto.
Qual deve ser o preço [tex]p[/tex], em reais, do pão especial nessa promoção?
Mais do que a resposta, confira a solução AQUI.
Problema 26:
Para resolver a equação [tex]36x^2 -12x +1 = 6x -1[/tex], Laila, uma aprendiz do matemático Beremiz, reescreveu esta equação como [tex](6x -1)^2 = 6x -1[/tex]. Daí, obteve [tex] 6x -1 = 1[/tex], de onde concluiu que a solução da equação original é [tex]x = \dfrac{2}{6}=\dfrac{1}{3}[/tex].
Beremiz a alertou para um erro de raciocínio e, então, Laila resolveu corretamente a equação.
Qual foi o erro e qual a solução correta?
Para resolver a equação [tex]36x^2 -12x +1 = 6x -1[/tex], Laila, uma aprendiz do matemático Beremiz, reescreveu esta equação como [tex](6x -1)^2 = 6x -1[/tex]. Daí, obteve [tex] 6x -1 = 1[/tex], de onde concluiu que a solução da equação original é [tex]x = \dfrac{2}{6}=\dfrac{1}{3}[/tex].
Beremiz a alertou para um erro de raciocínio e, então, Laila resolveu corretamente a equação.
Qual foi o erro e qual a solução correta?
Mais do que a resposta, confira a solução AQUI.
Problema 27:
Encontre as medidas dos catetos de um triângulo retângulo sabendo que sua hipotenusa tem comprimento de [tex]13[/tex] metros e um dos catetos tem comprimento [tex]7[/tex] metros maior do que o outro.
Encontre as medidas dos catetos de um triângulo retângulo sabendo que sua hipotenusa tem comprimento de [tex]13[/tex] metros e um dos catetos tem comprimento [tex]7[/tex] metros maior do que o outro.
Mais do que a resposta, confira a solução AQUI.
Problema 28:
Um grupo de amigos, numa excursão, aluga uma van por [tex]R$ \, 342,00[/tex], sendo que esse valor, a princípio, deveria ser dividido igualmente por todos.
Contudo, ao fim do passeio, três amigos estavam sem dinheiro e os outros tiveram que completar o total, pagando, cada um deles 19 reais a mais.
Quantos eram os amigos?
Um grupo de amigos, numa excursão, aluga uma van por [tex]R$ \, 342,00[/tex], sendo que esse valor, a princípio, deveria ser dividido igualmente por todos.
Contudo, ao fim do passeio, três amigos estavam sem dinheiro e os outros tiveram que completar o total, pagando, cada um deles 19 reais a mais.
Quantos eram os amigos?
Mais do que a resposta, confira a solução AQUI.
Equipe COM – OBMEP
