Clique no botão abaixo para visualizar a Sala.
Problema 1
(PUC-RIO 2008) Na sequência [tex](1, 3, 7,\cdots ),[/tex] cada termo é duas vezes o anterior mais um. Assim, por exemplo, o quarto termo é igual a [tex]15.[/tex] Determine o décimo termo.
[tex]~~\\
\qquad a_4 = 2\cdot a_3+1 = 2\cdot 7+1 = 15;\\
\qquad a_5 = 2\cdot a_4+1 = 2\cdot 15+1 = 31;\\
\qquad a_6 = 2\cdot a_5+1 = 2\cdot 31+1 = 63;\\
\qquad a_7 = 2\cdot a_6+1 = 2\cdot 63+1 = 127;\\
\qquad a_8 = 2\cdot a_7+1 = 2\cdot 127+1 = 255;\\
\qquad a_9 = 2\cdot a_8+1 = 2\cdot 255+1 = 511;\\
\qquad \boxed{a_{10} = 2\cdot a_9+1 = 2\cdot 511+1 = 1023}.[/tex]
Problema 2
(ITA 2000) O valor de [tex]n[/tex] que torna a sequência [tex](2 + 3n, -5n, 1 – 4n)[/tex] uma progressão aritmética pertence ao intervalo
a) [tex][-2, -1].[/tex]
b) [tex][-1, 0].[/tex]
c) [tex][0, 1].[/tex]
d) [tex][1, 2].[/tex]
e) [tex][2, 3].[/tex]
Assim, se [tex]a_1[/tex], [tex]a_2[/tex] e [tex]a_3[/tex] são os três primeiros termos dessa progressão, sabemos que:
[tex] \qquad a_2-a_1=r \text{ e } a_3-a_2=r.[/tex]
Dessa forma:
[tex] \qquad a_2-a_1=a_3-a_2\\
\qquad a_2+a_2=a_3+a_1\\
\qquad 2a_2=a_3+a_1\\
\qquad a_2=\dfrac{a_1+a_3}{2}.[/tex]
Como a sequência foi dada como [tex](2 + 3n, -5n, 1 – 4n)[/tex], segue que:
[tex]\qquad -5n=\dfrac{(2+3n)+(1-4n)}{2}[/tex]
[tex]\qquad -10n=(2+3n)+(1-4n)[/tex]
[tex]\qquad -10n=-n+3[/tex]
[tex]\qquad 9n=-3[/tex]
[tex]\qquad \boxed{n=-\dfrac{1}{3}}.[/tex]
Portanto, [tex]n\in [-1, 0][/tex] e a alternativa correta é a b.
Problema 3
(FUVEST 2012) Considere uma progressão aritmética cujos três primeiros termos são dados por:
[tex]\qquad a_1 = 1 + x, ~~a_2 = 6x, ~~a_3 = 2x^2 + 4,[/tex]
em que [tex]x[/tex] é um número real.
a) Determine os possíveis valores de [tex]x.[/tex]
b) Calcule a soma dos [tex]100[/tex] primeiros termos da progressão aritmética correspondente ao menor valor de [tex]x[/tex] encontrado no item a).
[tex]~~\\
\qquad 6x=\dfrac{(1+x)+(2x^2 + 4)}{2}[/tex]
[tex]\qquad 12x=(1+x)+(2x^2 + 4)[/tex]
[tex]\qquad 12x=2x^2+x+5[/tex]
[tex]\qquad 2x^2-11x+5=0.[/tex]
Utilizando a fórmula resolutiva para equações do segundo grau, temos:
[tex]\qquad x = \dfrac{-(-11)\pm \sqrt{(-11)^2-4\cdot 2\cdot 5}}{2\cdot 2}\\
\qquad x = \dfrac{11\pm \sqrt{121-40}}{4}\\
\qquad x = \dfrac{11\pm \sqrt{81}}{4}\\
\qquad x = \dfrac{11\pm 9}{4}[/tex]
[tex]\qquad x_1 = \dfrac{11+9}{4} = \dfrac{20}{4} = 5[/tex] e [tex]x_2 = \dfrac{11-9}{4} = \dfrac{2}{4} = \dfrac{1}{2}[/tex]
[tex]\qquad \boxed{x_1 = 5}[/tex] e [tex]\boxed{x_2 = \dfrac{1}{2}}.[/tex]
b) O menor valor de [tex]x[/tex] encontrado no item a) é [tex]x=\dfrac{1}{2}[/tex]. Neste caso,
[tex]\qquad a_1 = 1+x=1+\dfrac{1}{2}=\dfrac{3}{2}[/tex].
Além disso, a razão é
[tex]\qquad r = a_2-a_1=6x-(1+x)=5x-1=\dfrac{5}{2}-1=\dfrac{3}{2}[/tex].
Para calcularmos a soma dos primeiros 100 termos, observe que temos duas fórmulas: [tex]\boxed{a_n=a_1+(n-1)\cdot r}~[/tex] e [tex]~\boxed{S_n = \dfrac{(a_1+a_n)\cdot n}{2}}[/tex]; logo, segue que:
[tex]~~\\
\qquad S_n = \dfrac{(a_1+[a_1+(n-1)\cdot r])\cdot n}{2}\\
\qquad S_n = \dfrac{(2a_1+(n-1)\cdot r)\cdot n}{2}\\
\qquad S_n = na_1+\dfrac{n(n-1)}{2}\cdot r.\\
~~[/tex]
Portanto, a soma dos primeiros 100 termos da P.A., é
[tex]\qquad S_{100} = 100\cdot \dfrac{3}{2}+\dfrac{100\cdot 99}{2}\cdot \dfrac{3}{2}[/tex]
[tex]\qquad S_{100} = 150+4950\cdot \dfrac{3}{2}[/tex]
[tex]\qquad S_{100} = 150+7425[/tex]
[tex]\qquad \boxed{S_{100} = 7575}.[/tex]
Problema 4
(Unicamp 2015 – Adaptada) Se [tex](a_1, a_2, \cdots, a_{13})[/tex] é uma progressão aritmética (PA) cuja soma dos termos é igual a [tex]78,[/tex] determine o valor de [tex]a_7[/tex].
Mas sabemos que [tex]\boxed{a_n=a_1+(n-1)\cdot r}[/tex]; logo, segue que
[tex]~~\\
\qquad S_n = \dfrac{(a_1+[a_1+(n-1)\cdot r])\cdot n}{2}\\
\qquad S_n = \dfrac{(2a_1+(n-1)\cdot r)\cdot n}{2}\\
\qquad S_n = na_1+\dfrac{n(n-1)}{2}\cdot r.\\
~~[/tex]
Assim, pelos dados do enunciado, segue que:
[tex]\qquad S_{13} = 13\cdot a_1+\dfrac{13\cdot 12}{2}\cdot r\\
\qquad 78 = 13\cdot (a_1+6\cdot r)\\
\qquad a_1+6\cdot r= 6\\
\qquad \boxed{a_7 = 6}.[/tex]
Problema 5
O triângulo retângulo representado na figura abaixo apresenta um perímetro igual a [tex]48~cm[/tex] e área igual a [tex]96~cm^2.[/tex] Quais são as medidas de [tex]x, y[/tex] e [tex]z,[/tex] se, nesta ordem, esses números formam uma PA?
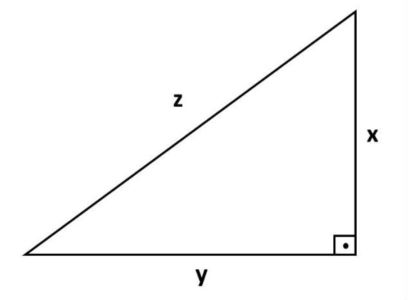
Observe que o triângulo da figura é retângulo; logo o segmento de comprimento [tex]x[/tex] pode ser considerado a altura do triângulo relativa ao segmento de comprimento [tex]y.[/tex]
Portanto, temos o sistema
[tex]\\
\qquad S: \begin{cases}
x+y+z=48\\
\dfrac{x\cdot y}{2}=96
\end{cases}.\\
[/tex]
Como [tex]x,~y[/tex] e [tex]z[/tex] formam uma P.A., então [tex]y=x+r~[/tex] e [tex]~z=x+2r[/tex]. Substituindo essas expressões em [tex]S[/tex], segue que:
[tex]\\
\qquad \begin{cases}
x+(x+r)+(x+2r)=48\\
\dfrac{x\cdot (x+r)}{2}=96
\end{cases}\\
[/tex]
[tex]\qquad \begin{cases}x+r=16\qquad \textcolor{#800000}{(i)}\\
x\cdot (x+r)=192 \qquad \textcolor{#800000}{(ii)}
\end{cases}.\\
[/tex]
Substituindo [tex]\textcolor{#800000}{(i)}[/tex] em [tex]\textcolor{#800000}{(ii)}[/tex], obtemos
[tex]\qquad x\cdot 16=192\\
\qquad \boxed{x=12}.\\
[/tex]
Agora, substituindo o valor de [tex]x[/tex] na igualdade [tex]x+r=16[/tex], encontramos [tex]r=4.[/tex]
Logo, [tex]\boxed{y = 16}~[/tex] e [tex]~\boxed{z=20}.[/tex]
Problema 6
(FUVEST 2008 – Adaptada) Numa progressão geométrica de quatro termos positivos, a soma dos dois primeiros vale [tex]1[/tex] e a soma dos dois últimos vale [tex]9.[/tex] Calcule a razão da progressão.
Podemos, então, montar o seguinte sistema de equações:
[tex]\\
\qquad \begin{cases}
a_1+a_2 = 1\\
a_3+a_4=9
\end{cases}.\\
[/tex]
Como a progressão é geométrica, se [tex]q[/tex] for a sua razão, segue que:
[tex]\\
\qquad\begin{cases}
a_1+a_1\cdot q = 1\\
a_1\cdot q^2+a_1\cdot q^3=9
\end{cases}~\\
[/tex]
[tex]\\
\qquad\begin{cases}
a_1\cdot (1+q) = 1\\
a_1q^2\cdot (1+q)=9
\end{cases}~\\
[/tex]
[tex]\\
\qquad\begin{cases}
a_1\cdot (1+q) = 1\qquad \textcolor{#800000}{(i)}\\
q^2\cdot[a_1\cdot (1+q)]=9 \qquad \textcolor{#800000}{(ii)}
\end{cases}~.[/tex]
Substituindo [tex]\textcolor{#800000}{(i)}[/tex] em [tex]\textcolor{#800000}{(ii)}[/tex], obtemos
[tex]\\
\qquad q^2\cdot 1=9\Rightarrow q^2=9\\
\qquad q=\pm 3.[/tex]
Como o enunciado nos informa que os termos da progressão são todos positivos, então devemos desconsiderar [tex]q=-3[/tex]; pois, caso o fosse, teríamos uma P.G. oscilante, o que não é o caso. Logo, [tex]\boxed{q=3}.[/tex]
Problema 7
(UFRGS 2015) Para fazer a aposta mínima na Mega-Sena, uma pessoa deve escolher [tex]6[/tex] números diferentes em um cartão de apostas que contém os números de [tex]1[/tex] a [tex]60.[/tex] Uma pessoa escolheu os números de sua aposta, formando uma progressão geométrica de razão inteira.
Com esse critério, é correto afirmar que:
a) essa pessoa apostou no número [tex]1.[/tex]
b) a razão da PG é maior do que [tex]3.[/tex]
c) essa pessoa apostou no número [tex]60.[/tex]
d) a razão da PG é [tex]3.[/tex]
e) essa pessoa apostou somente em números ímpares.
Observe, inicialmente, que:
- a razão [tex]q[/tex] é um número natural;
- [tex]q\neq 0[/tex]; pois, caso contrário, teríamos cinco termos iguais a [tex]0[/tex] e isso não pode ocorrer, já que todos os seis termos devem ser diferentes e, de [tex]1[/tex] a [tex]60[/tex]);
- [tex]q\neq 1[/tex], pois se fosse [tex]q=1[/tex], teríamos todos os números iguais.
Assim, devemos ter [tex]q\geq 2.[/tex] No entanto, perceba que
- para [tex]q=3[/tex] teríamos [tex]a_5= a_1\cdot q^4=81a_1[/tex]. Portanto, ainda que tivéssemos [tex]a_1=1[/tex], teríamos [tex]a_5=81[/tex], o que também não pode ocorrer, já que o maior número disponível para fazer aposta é [tex]60[/tex], ou seja, [tex]q[/tex] não pode ser igual a [tex]3[/tex], tampouco um número maior. Logo, [tex]\boxed{q=2}.[/tex]
Com isso, já podemos descartar os itens b), d) e e).
- Agora, repare que se essa pessoa tiver apostado no número [tex]60[/tex], então este teria sido o maior número apostado, ou seja, [tex]a_6[/tex]. Consequentemente, teríamos [tex]a_5=\dfrac{60}{2}=30; ~~a_4=\dfrac{30}{2}=15; ~~a_3=\dfrac{15}{2}=7,5;[/tex] e, portanto, novamente teríamos um problema, pois todos os números apostados devem ser números inteiros.
Logo, o item correto é a).
Com efeito, se tivéssemos [tex]a_1\geq 2[/tex], então [tex]a_6 = a_1\cdot q^5=32a_1\geq 64[/tex], o que também não pode ocorrer.
Assim, de fato, [tex]a_1=1[/tex] e, consequentemente, os números apostados foram: [tex]1~,2,~4,~8,~16 \text{ e }32.[/tex]
Problema 8
(PUC/RIO 2017 – Adaptada) Os termos da soma [tex]S = 4 + 8 + 16 +\cdots + 2048[/tex] estão em progressão geométrica. Determine o valor de [tex]S[/tex].
[tex]\qquad a_n=2048[/tex]
[tex]\qquad a_1\cdot q^{n-1}=2048[/tex]
[tex]\qquad 4\cdot 2^{n-1}=2048[/tex]
[tex]\qquad 2^{n+1}=2048[/tex]
[tex]\qquad 2^{n+1}=2^{11}[/tex]
[tex]\qquad n+1=11[/tex]
[tex]\qquad n=10.[/tex]
Assim, como a P.G. tem 10 termos, já podemos usar a fórmula da soma dos termos da P.G.:
[tex]\qquad S = S_{10}=\dfrac{4\cdot (2^{10}-1)}{2-1}\\
\qquad S = 4\cdot 1023\\
\qquad \boxed{S = 4092}.[/tex]
Problema 9
(UERJ 2014 – Adaptada) Em um recipiente com a forma de um paralelepípedo retângulo com [tex]40\text{ cm}[/tex] de comprimento, [tex]25\text{ cm}[/tex] de largura e [tex]20\text{ cm}[/tex] de altura, foram depositadas, em etapas, pequenas esferas, cada uma com volume igual a [tex]0,5\text{ cm}^3.[/tex] Na primeira etapa, depositou-se uma esfera; na segunda, duas; na terceira, quatro; e assim sucessivamente, dobrando-se o número de esferas a cada etapa.
Admita que, quando o recipiente está cheio, o espaço vazio entre as esferas é desprezível.
Aproximadamente, quantas etapas serão necessárias para que o volume total de esferas seja maior do que o volume do recipiente?
- A sequência cujos termos indicam o volume de bolinhas que está sendo acrescentado no recipiente a cada etapa é
[tex]\qquad (0,5;~0,5\cdot 2;~0,5\cdot 2^2;~0,5\cdot 2^3;~\cdots).[/tex] - O volume do recipiente no qual as esferas estão sendo colocadas é
[tex] \qquad 40\times 25\times 20 = 20\;000\;\text{cm}^3.[/tex]
Assim, se [tex]n[/tex] é o número mínimo de etapas tal que o volume total de esferas seja maior do que o volume do recipiente, segue que:
[tex]\qquad 0,5+0,5\cdot 2+0,5\cdot 2^2+0,5\cdot 2^3+\cdots+0,5\cdot 2^{n-1}\gt 20\;000\\
\qquad S_n\gt 20\;000\\
\qquad \dfrac{0,5\cdot (2^n-1)}{2-1}\gt 20\;000\\
\qquad 0,5\cdot (2^n-1)\gt 20\;000\\
\qquad 2^n-1\gt 40\;000\\
\qquad 2^n\gt 40\;001.[/tex]
Agora, observe que [tex]2^{15} = 32\;768~[/tex] e [tex]~2^{16} = 65\;536;[/tex] logo, devemos ter [tex]2^n= 2^{16}[/tex], ou seja, [tex]\boxed{n=16}.[/tex]
Portanto, o menor número de etapas é [tex]16.[/tex]
Problema 10
(UNICAMP 2015 – Adaptada) Seja [tex](a, b, c)[/tex] uma progressão geométrica de números reais com [tex]a\neq 0.[/tex] Definindo [tex]s = a + b + c,[/tex] determine o menor valor possível para [tex]\dfrac{s}{a}[/tex].
[tex]\qquad \dfrac{s}{a}=\dfrac{a+b+c}{a}\\
\qquad \dfrac{s}{a}=\dfrac{a+aq+aq^2}{a}\\
\qquad \dfrac{s}{a}=\dfrac{a(1+q+q^2)}{a}\\
\qquad \dfrac{s}{a}=1+q+q^2.[/tex]
Considere a função [tex]f[/tex] definida por [tex]f(q) = 1+q+q^2[/tex] e observe que o menor valor de [tex]\dfrac{s}{a}[/tex] ocorre quando [tex]f(q) = 1+q+q^2[/tex] admite o menor valor possível.
Repare que [tex]f[/tex] é uma função quadrática cujo gráfico é uma parábola com concavidade voltada para cima. Assim, o menor valor possível de [tex]\dfrac{s}{a}[/tex] é dado pela coordenada “[tex]y[/tex] do vértice da parábola” ([tex]y_v[/tex]); então, vamos calcular esse valor:
[tex]\qquad y_v=-\dfrac{\Delta}{4a}\\
\qquad y_v=-\dfrac{b^2-4ac}{4a}\\
\qquad y_v=-\dfrac{1^2-4\cdot 1\cdot 1}{4\cdot 1}\\
\qquad y_v=-\dfrac{-3}{4}\\
\qquad \boxed{y_v=\dfrac{3}{4}}.[/tex]
Problema 11
(Enem 2011 – Adaptada) O número mensal de passagens vendidas de uma determinada empresa aérea aumentou no ano passado nas seguintes condições: em janeiro foram vendidas [tex]33\,000[/tex] passagens; em fevereiro, [tex]34\,500;[/tex] em março, [tex]36\,000.[/tex] Esse padrão de crescimento se manteve nos meses subsequentes. Quantas passagens foram vendidas por essa empresa em julho do ano passado?
A quantidade de passagens vendidas no mês de julho corresponde ao sétimo termo dessa P.A. e
[tex]\qquad a_7 = 33\;000+6\cdot 1\;500[/tex]
[tex]\qquad a_7 = 33\;000+9\;000[/tex]
[tex]\qquad a_7 = 42\;000.[/tex]
Logo, em julho foram vendidas [tex]42\;000[/tex] passagens.
Problema 12
(Enem 2012 – Adaptada) Jogar baralho é uma atividade que estimula o raciocínio. Um jogo tradicional é a Paciência, que utiliza [tex]52[/tex] cartas. Inicialmente são formadas sete colunas com as cartas. A primeira coluna tem uma carta, a segunda tem duas cartas, a terceira tem três cartas, a quarta tem quatro cartas, e assim sucessivamente até a sétima coluna, a qual tem sete cartas, e o que sobra forma o monte, que são as cartas não utilizadas nas colunas.
Quantas cartas formam o monte?
Assim, a soma do total de cartas nas colunas é dada por:
[tex]\qquad S_7 = \dfrac{(1+7)\cdot 7}{2}\\
\qquad S_7 = 28.[/tex]
Portanto o total de cartas no monte é [tex]52-28=\boxed{24}.[/tex]
Problema 13
(Enem 2016 – Adaptada) Sob a orientação de um mestre de obras, João e Pedro trabalharam na reforma de um edifício. João efetuou reparos na parte hidráulica nos andares [tex]1, 3, 5, 7,[/tex] e assim sucessivamente, de dois em dois andares. Pedro trabalhou na parte elétrica nos andares [tex]1, 4, 7, 10,[/tex] e assim sucessivamente, de três em três andares. Coincidentemente, terminaram seus trabalhos no último andar. Na conclusão da reforma, o mestre de obras informou, em seu relatório, o número de andares do edifício. Sabe-se que, ao longo da execução da obra, em exatamente [tex]10[/tex] andares, foram realizados reparos nas partes hidráulica e elétrica por João e Pedro. Qual é o número de andares desse edifício?
Assim, o número de andares desse edifício corresponde ao décimo termo da P.A. acima. Portanto,
[tex]\qquad a_{10} = 1+(10-1)\cdot 6\\
\qquad a_{10} = 1+9\cdot 6\\
\qquad \boxed{a_{10} = 55}[/tex]
e, com isso, concluímos que o edifício possui [tex]55[/tex] andares.
Problema 14
(Enem 2018 – Adaptada) A prefeitura de um pequeno município do interior decide colocar postes para iluminação ao longo de uma estrada retilínea, que inicia em uma praça central e termina numa fazenda na zona rural. Como a praça já possui iluminação, o primeiro poste será colocado a [tex]80[/tex] metros dela, o segundo, a [tex]100[/tex] metros, o terceiro, a [tex]120[/tex] metros, e assim sucessivamente, mantendo-se sempre uma distância de [tex]20[/tex] metros entre os postes, até que o último poste seja colocado a uma distância de [tex]1\;380[/tex] metros da praça.
Se a prefeitura pode pagar, no máximo, [tex]R$~8\,000[/tex] por poste colocado, determine o maior valor que poderá gastar com a colocação desses postes.
Seja [tex]a_n[/tex] o último termo da sequência, ou seja, [tex]a_n = 1\;380.[/tex] Pela fórmula do termo geral de uma P.A., temos
[tex]\qquad a_n = 1\;380\\
\qquad a_1+(n-1)\cdot r= 1\;380\\
\qquad 80+(n-1)\cdot 20= 1\;380\\
\qquad (n-1)\cdot 20= 1\;300\\
\qquad (n-1)= 65\\
\qquad n= 66,[/tex]
ou seja, deverão ser instalados [tex]66[/tex] postes.
Como o valor máximo que pode ser gasto para colocar cada poste corresponde a [tex]R$~8\,000[/tex], então o valor máximo para colocar os [tex]66[/tex] postes é dado pelo produto [tex]66\times 8\;000 = 528\;000, [/tex] ou seja, [tex] \boxed{R$~528\;000}.[/tex]
Problema 15
(UEPA – Adaptada) Um carro, cujo preço à vista é [tex]R$ ~24\,000,00,[/tex] pode ser adquirido dando-se uma entrada e o restante em [tex]5[/tex] parcelas que se encontram em progressão geométrica. Um cliente que optou por esse plano, ao pagar a entrada, foi informado que a segunda parcela seria de [tex]R$ ~4\,000,00[/tex] e a quarta parcela de [tex]R$ ~1\,000,00.[/tex] Sabendo que no valor das parcelas não incidiu taxa de juros, quanto esse cliente pagou de entrada na aquisição desse carro?
[tex]\quad (a_1, 4\;000, a_3, 1\;000, a_5).[/tex]
Neste caso, pela propriedade que vimos de P.G., temos
[tex]\quad a_3 = \sqrt{4\;000\times 1\;000}[/tex]
[tex]\quad \boxed{a_3 = 2\;000}.[/tex]
Portanto, a razão [tex]q[/tex] é dada por:
[tex]\quad q = \dfrac{a_3}{a_2} = \dfrac{2\;000}{4\;000} = \dfrac{1}{2}.[/tex]
Como [tex]a_2 = a_1q[/tex], segue que:
[tex]\quad 4\;000 = a_1\cdot \dfrac{1}{2}\\
\quad \boxed{a_1 = 8\;000}.[/tex]
Por fim, o último termo da P.G. é dado por
[tex]\quad a_5 = a_4\cdot q\\
\quad a_5= 1\;000\cdot \dfrac{1}{2}\\
\quad \boxed{a_5=500}.[/tex]
Logo, o valor pago de entrada foi
[tex]\quad Entrada=24\;000-(8\;000+4\;000+2\;000+1\;000+500)\\
\quad Entrada= 24\;000-15\;500\\
\quad Entrada = \boxed{R$~8\;500}.[/tex]
Equipe COM – OBMEP
