Clique no botão abaixo para visualizar a Sala.
Algumas funções podem ser classificadas quanto às suas leis de formação.
Nesta Sala, vamos apresentar algumas dessas funções e tentar aplicar o que foi discutido nas duas primeiras Salas.
Vamos começar com a mais simples delas!
I – Função Constante
Gráfico: O gráfico de uma função constante traçado em um plano cartesiano [tex]xOy[/tex] é uma reta perpendicular ao eixo [tex]Oy[/tex] e, portanto, paralela ao eixo [tex]Ox[/tex], que intersecta [tex]Oy[/tex] no ponto [tex](0,c)[/tex].
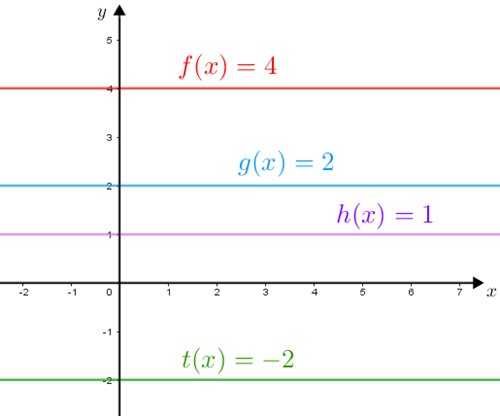
Como já havíamos comentado, uma função constante é vista como o tipo mais simples de função. Observando esses gráficos dá para entender o porquê, não é?
Particularmente, uma função constante
● não é injetora;
● não é sobrejetora;
● não é crescente;
● não é decrescente.
II – Função Afim
Antes de apresentarmos a definição de função afim, vamos ver um exemplo prático que está relacionado a esse tipo de função.
A comissão de Joel é calculada com base em uma taxa fixa de [tex]3\%[/tex] sobre o valor total das vendas que ele realizar no mês.
Vamos escrever uma expressão que relacione o salário mensal [tex]s[/tex] de Joel com o valor [tex]v[/tex] de suas vendas mensais.
A comissão de Joel é dada por [tex]3\%[/tex] de [tex]v[/tex], ou seja, [tex]\dfrac{3}{100}v.[/tex] Como ele ganha um valor fixo de [tex]R$\,1\;500,00[/tex] por mês além da comissão, então representando por [tex]s(v)[/tex] o salário de Joel em termos do valor [tex]v[/tex] de suas vendas, temos:
[tex]\qquad \boxed{s(v) = \dfrac{3}{100}v+1\;500}.[/tex]
Gráfico: O gráfico de uma função afim traçado em um plano cartesiano [tex]xOy[/tex] é uma reta oblíqua aos eixos [tex]Ox\,[/tex] e [tex]\,Oy[/tex].
Sendo [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]f(x) = ax+b[/tex], com [tex]a\ne 0[/tex], podemos perceber que:
● [tex]f(0) = a\cdot 0+b = b[/tex].
● Os zeros de [tex]f[/tex] são tais que [tex]f(x)=0[/tex]. Assim, temos [tex]ax+b = 0[/tex], ou seja, [tex]x = -\dfrac{b}{a}[/tex].
Assim, o gráfico de [tex]f[/tex] é a reta que passa pelos pontos [tex](0, b)[/tex] e [tex]\left(-\dfrac{b}{a}, 0\right)[/tex].
A partir dessas informações e dependendo dos sinais dos coeficientes [tex]a~[/tex] e [tex]~b[/tex], temos os seguintes gráficos para a função [tex]f[/tex], se [tex]b\ne 0[/tex]:
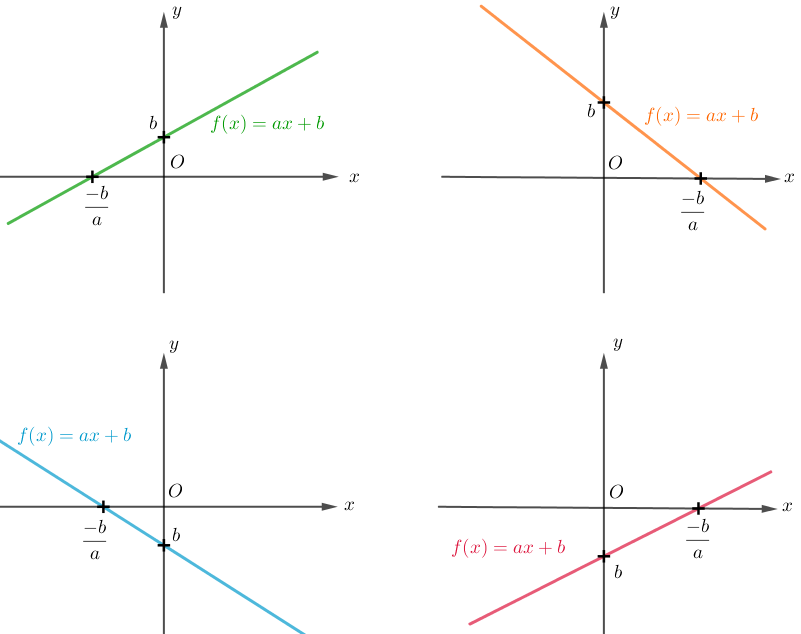
e se, particularmente, [tex]b=0[/tex] são estes os gráficos:

Vamos agora procurar saber em quais casos a função afim é crescente e quando é decrescente. A visualização dos gráficos acima vai ajudar na visualização das análises!
Seja [tex]f[/tex] uma função afim dada por [tex]f(x) = ax+b[/tex] e [tex]x_1,x_2\in D(f)[/tex], com [tex]x_1\lt x_2 [/tex]. Perceba que:
► [tex]f(x_1)\lt f(x_2) \iff ax_1+b\lt ax_2+b\iff ax_1\lt ax_2\iff a\gt 0[/tex],
sendo que a última equivalência acima decorre do fato de termos [tex]x_1\lt x_2[/tex];
► [tex]f(x_1)\gt f(x_2) \iff ax_1+b\gt ax_2+b\iff ax_1\gt ax_2\iff a\lt 0[/tex],
sendo que a última equivalência acima decorre do fato de termos [tex]x_1\lt x_2.[/tex]
Portanto, podemos concluir que, se [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] é dada por [tex]f(x) = ax+b[/tex], então
● [tex]\boldsymbol{f}[/tex] é crescente se, e somente se, [tex]\boldsymbol{ a\gt 0} [/tex], e
● [tex]\boldsymbol{f}[/tex] é decrescente se, e somente se, [tex]\boldsymbol{ a\lt 0 }[/tex].
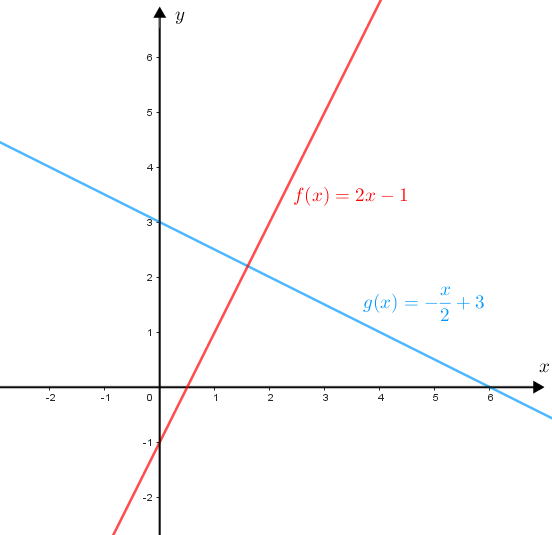
Exemplo 2: A função afim [tex]g:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]g(x)=-\dfrac{x}{2}+3[/tex] é decrescente, pois [tex]a=-\dfrac{1}{2}\lt 0[/tex].
Vejam os gráficos!
Quanto à injetividade e à sobrejetividade de uma função afim [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]f(x)=ax+b,~a\ne 0[/tex], observe que:
- (i) Sejam [tex]x_1,x_2\in \mathbb{R}[/tex] tais que [tex]\boxed{f(x_1)=f(x_2)}.[/tex]
Assim, segue que:
[tex]\qquad ax_1+b=ax_2+b\\
\qquad ax_1=ax_2\\
\qquad \boxed{x_1=x_2}.[/tex]
(ii) Seja [tex]\boxed{y \in \mathbb{R}}[/tex]. Perceba que, se [tex]\boxed{x=\dfrac{y-b}{a}}[/tex], então:
[tex]\qquad f(x)=f\left(\dfrac{y-b}{a}\right)\\
\qquad f(x)=a\left(\dfrac{y-b}{a}\right)+b\\
\qquad f(x)=y-b+b\\
\qquad \boxed{f(x)=y}.
[/tex]
Portanto, por (i) e (ii) podemos concluir que:
● uma função afim é injetora e
● uma função afim é sobrejetora
SEMPRE!
III – Função Quadrática
Gráfico: O gráfico de uma função quadrática é uma parábola, podendo ela ter a concavidade voltada para cima (caso [tex]a\gt 0[/tex]) ou para baixo (caso [tex]a\lt 0[/tex]).
Você pode utilizar este applet para observar as concavidades de algumas parábolas e verificar que, de fato, a concavidade voltada para cima ou para baixo está ligada ao sinal do coeficiente [tex]a[/tex] de [tex]x^2.[/tex]
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para mudar manualmente os valores de [tex]a[/tex] e obter as parábolas correspondentes, clique com o botão esquerdo do mouse sobre o ponto que indica o valor de a (lado direito da janelinha), mantenha o botão apertado e, em seguida, movimente o mouse horizontalmente. (Se você estiver utilizando um celular ou um tablet, toque levemente no ponto e movimente-o.)
(3) Para fazer uma animação do movimento do ponto a e obter novas parábolas, clique no ícone ► que aparece no canto inferior esquerdo da janela.
(4) Para parar a animação, clique no ícone || que apareceu no canto inferior esquerdo da janela.
(5) Se quiser voltar para a visualização inicial, clique nas setinhas circulares que aparecem no canto superior direito da janela.
OBMEP_ srdg, criado com o GeoGebra
Observações: O GeoGebra trabalha com arredondamentos. A visualização de várias situações particulares de um fato matemático não substitui sua demonstração.
Podemos reescrever a expressão [tex]~f(x)=ax^2+bx+c~[/tex] que define a função quadrática [tex]f[/tex] de uma outra maneira; observe:
[tex]\qquad\begin{align}
f(x) &= ax^2+bx+c\\
&= a\left(x^2+\dfrac{b}{a}x+\dfrac{c}{a}\right)\\
&= a\left(x^2+2\dfrac{b}{2a}x+\dfrac{c}{a}\right)\\
&= a\left(x^2+2\dfrac{b}{2a}x+\dfrac{b^2}{4a^2}-\dfrac{b^2}{4a^2}+\dfrac{c}{a}\right)\\
&= a\left[\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2}{4a^2}+\dfrac{c}{a}\right]\\
&= a\left[\left(x+\dfrac{b}{2a}\right)^2-\left(\dfrac{b^2}{4a^2}-\dfrac{c}{a}\right)\right]\\
&= a\left[\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2-4ac}{4a^2}\right].
\end{align}[/tex]
Assim, [tex]f(x) = a\left[\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2-4ac}{4a^2}\right][/tex], e essa maneira de representar a função quadrática é chamada de Forma Canônica da Função Quadrática.
Podemos usar essa Forma Canônica para obter as raízes da função quadrática [tex]f[/tex]:
[tex]\qquad \begin{align}
f(x) = 0 &\iff a\left[\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2-4ac}{4a^2}\right] = 0\\
&\iff \left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2-4ac}{4a^2} = 0\\
&\iff \left(x+\dfrac{b}{2a}\right)^2 = \dfrac{b^2-4ac}{4a^2}\\
&\iff x+\dfrac{b}{2a} = \pm\sqrt{\dfrac{b^2-4ac}{4a^2}}\\
&\iff x = -\dfrac{b}{2a}\pm\dfrac{\sqrt{b^2-4ac}}{2a}\\
&\iff x = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a},\\
\end{align} [/tex]
ou seja,
[tex]\qquad f(x) = 0 \iff \boxed{x=\dfrac{-b\pm\sqrt{\Delta}}{2a}}[/tex], sendo [tex]\Delta = b^2-4ac[/tex].
Muitas pessoas se referem equivocadamente a essa fórmula como “fórmula de Bháskara”; no entanto não existe nenhuma comprovação científica de que tal ferramenta foi desenvolvida por Bháskara (aproximadamente, 1114-1185), matemático, astrônomo e astrólogo indiano. Assim, chamaremos a fórmula acima de fórmula resolutiva de equações do 2º grau, uma vez que encontrar as raízes de uma função quadrática significa resolver a equação do 2º grau associada à ela.
Vejamos alguns exemplos:
[tex]\qquad x = \dfrac{-1\pm\sqrt{1^2-4\cdot 1\cdot (-1)}}{2\cdot 1}\\
\qquad x = \dfrac{-1\pm\sqrt{5}}{2}\\
\qquad x_1 = \dfrac{-1-\sqrt{5}}{2}~~\text{ e }~~x_2 = \dfrac{-1+\sqrt{5}}{2}.[/tex]
Isso implica que o gráfico da função intersecta o eixo das abcissas nos valores [tex]\dfrac{-1-\sqrt{5}}{2}~[/tex] e [tex]~\dfrac{-1+\sqrt{5}}{2}.[/tex]
► Na função [tex]g: \mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]g(x) = x^2-2x+1[/tex], temos [tex]a=1,~b=-2~[/tex] e [tex]~c=1[/tex]; assim, as raízes dessa função são dadas por:
[tex]\qquad x = \dfrac{2\pm\sqrt{(-2)^2-4\cdot 1\cdot (1)}}{2\cdot 1}\\
\qquad x = \dfrac{2\pm\sqrt{0}}{2}.[/tex]
Aqui temos apenas uma raiz:
[tex] \qquad x_1 = 1[/tex]
e, então, o gráfico da função intersecta o eixo das abcissas apenas em [tex]1.[/tex]
► Na função [tex]h: \mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x) = x^2-x+3[/tex], temos [tex]a=1,~b=-1~[/tex] e [tex]~c=3[/tex]; assim, as raízes dessa função são dadas por:
[tex]\qquad x = \dfrac{1\pm\sqrt{(-1)^2-4\cdot 1\cdot (3)}}{2\cdot 1}\\
\qquad x = \dfrac{2\pm\sqrt{-11}}{2}.[/tex]
Aqui temos um enrosco: como o domínio da função [tex]h[/tex] é [tex]\mathbb{R}[/tex], então as raízes de [tex]h[/tex] devem ser números reais, não é? Mas sabemos que [tex]\sqrt{-11} \not\in \mathbb{R}[/tex] e, portanto, a função [tex]h[/tex] não tem raízes!
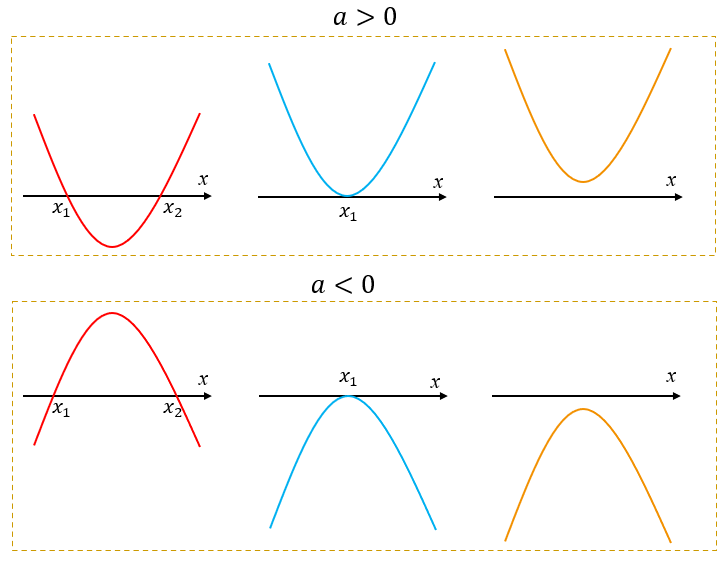
Esses últimos exemplos ilustram as três situações que podemos ter com relação às raízes de funções quadráticas. Se [tex]f: \mathbb{R}\rightarrow \mathbb{R}[/tex] é a função quadrática definida por [tex]f(x) = ax^2+bx+c[/tex], então, ao analisar o valor do respectivo [tex]\Delta[/tex] podemos encontrar três situações:
● [tex]\Delta \gt 0[/tex] e [tex]f[/tex] tem duas raízes reais;
● [tex]\Delta = 0[/tex] e [tex]f[/tex] tem apenas uma raiz real;
● [tex]\Delta \lt 0[/tex] e [tex]f[/tex] não tem raízes reais.
Assim, geometricamente, temos três situações aliadas ao sinal do coeficiente [tex]a[/tex], conforme ilustram as imagens a seguir.
Para dar continuidade à nossa discussão, vamos apresentar um problema que envolve o conceito de função quadrática:
Para resolver esse problema, vamos precisar falar sobre o vértice de uma parábola.
Você vai perceber mais adiante na imagem com a ilustração das concavidades dos gráficos que, quando [tex]a\gt 0[/tex], ou seja, quando a concavidade está voltada para cima, a função admite um valor mínimo; o que implica na existência de [tex]k\in D(f)[/tex], tal que [tex]f(k)\leq f(x)[/tex], para todo [tex]x\in D(f)[/tex]. O ponto no gráfico que indica a existência desse valor mínimo é o de coordenadas [tex](k,f(k))[/tex], que é o ponto que possui menor altura.
Podemos verificar na forma canônica da função que o termo [tex]\left(x+\dfrac{b}{2a}\right)^2[/tex] é não negativo, independentemente do valor de [tex]x[/tex]; assim, se [tex]a\gt 0[/tex], então o valor mínimo ocorre quando [tex]\left(x+\dfrac{b}{2a}\right)^2=0[/tex], ou seja, a função quadrática com [tex]a\gt 0[/tex] admite menor valor quando [tex]x = -\dfrac{b}{2a}[/tex].
Assim, quando [tex]x = -\dfrac{b}{2a}[/tex], temos
[tex]\qquad f(x) = a\left[\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2-4ac}{4a^2}\right]= a\left[0^2-\dfrac{b^2-4ac}{4a^2}\right] = -\dfrac{b^2-4ac}{4a},[/tex]
ou seja, o menor valor que a função pode admitir neste caso é [tex]~-\dfrac{\Delta}{4a}[/tex], sendo [tex]\Delta = b^2-4ac[/tex].
De forma análoga podemos mostrar que as fórmulas são as mesmas para o caso em que [tex]a\lt 0[/tex], ou seja, para o caso em que a função admite um valor máximo.
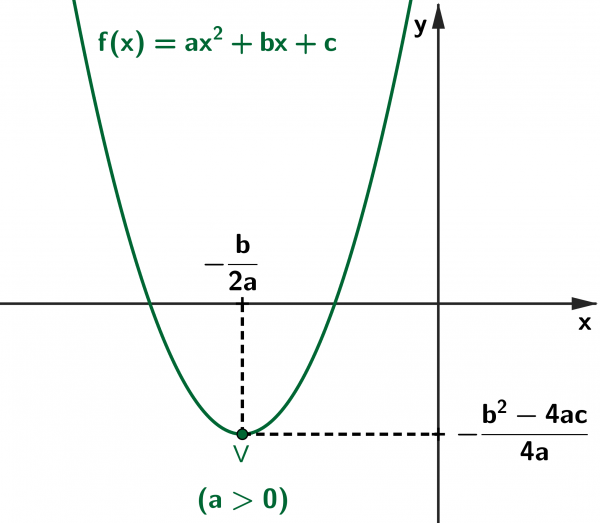
O ponto, no gráfico da função, associado ao menor (ou maior) valor que uma função quadrática [tex]f[/tex] de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex] admite é chamado de vértice da parábola e é representado por [tex]V[/tex] nos dois casos ([tex]a\gt 0[/tex] e [tex]a\lt 0[/tex]), na figura abaixo.
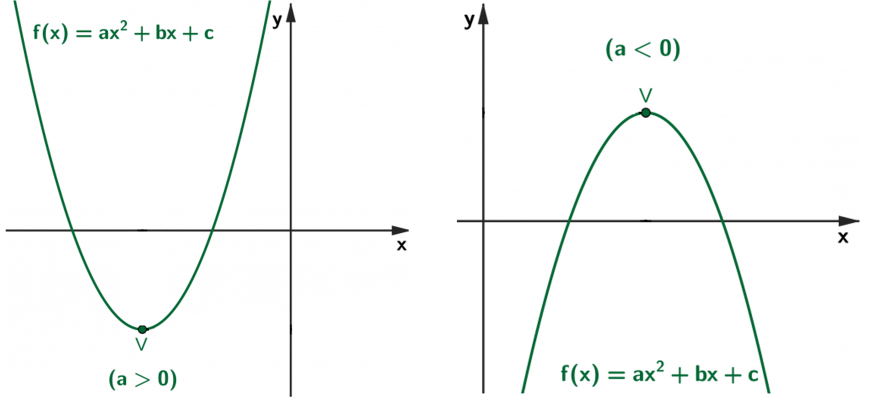
Portanto, sendo [tex](x_v,y_v)[/tex] as coordenadas do vértice V da parábola, temos [tex](x_v,y_v) = \left(-\dfrac{b}{2a},\dfrac{-\Delta}{4a}\right)[/tex].
Graficamente, se [tex]a\gt 0[/tex] temos um gráfico deste tipo
enquanto que, se [tex]a\lt 0[/tex] é este o tipo de gráfico da função quadrática:

Substituindo na fórmula, temos [tex]t=-\dfrac{20}{2(-5)} = 2[/tex] segundos. A altura máxima será [tex]h(2) = -5\cdot 2^2 + 20\cdot 2 = 20[/tex] metros.
A partir da segunda coordenada do vértice de uma parábola, podemos garantir que qualquer função quadrática definida de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex] não é sobrejetora; pois, dependendo do sinal de [tex]a[/tex], há duas possibilidades para o conjunto imagem da função definida por [tex]f(x)=ax^2+bx+c[/tex], com [tex]a \ne 0:[/tex]
|
► Para [tex]a \gt 0[/tex] temos: [tex]Im(f)=\left\{y \in \mathbb{R}~|~y \geqslant y_v=- \dfrac{\Delta}{4a} \right\}[/tex] 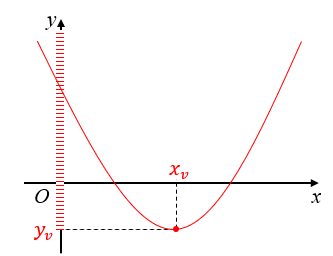
|
► Para [tex]a \lt 0[/tex] temos: [tex]Im(f)=\left\{y \in \mathbb{R}~|~y \leqslant y_v=- \dfrac{\Delta}{4a} \right\}[/tex] 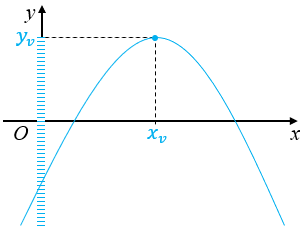
|
De toda forma, [tex]Im(f)\ne \mathbb{R}=CD(f).[/tex]
Por outro lado, qualquer função quadrática não é injetora. A própria simetria da parábola em relação à reta vertical que passa pelo vértice nos garante que o único valor de [tex]y[/tex] que é imagem de um único valor de [tex]x[/tex] é o [tex]y_v.[/tex] Podemos também visualizar a não injetividade de uma função quadrática traçando as “famosas” retas horizontais para verificar que, com exceção da reta [tex]y=y_v[/tex], elas cortam a parábola em dois pontos, conforme ilustram as imagens a seguir.
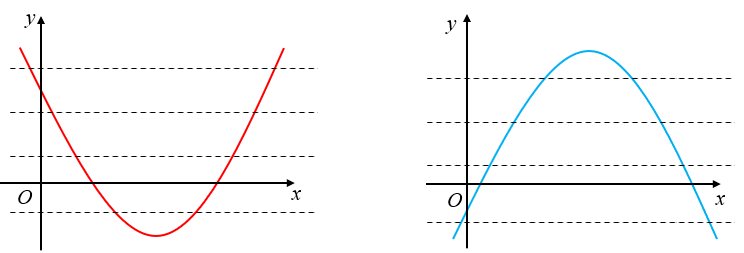
Pelo exposto, podemos afirmar que:
● Toda função quadrática não é sobrejetora.
● Toda função quadrática não é injetora.
Observado o gráfico de uma função quadrática, é possível perceber que esse tipo de função não é crescente e nem decrescente, embora tenha regiões de crescimento e de decrescimento facilmente detectadas a partir do vértice de sua parábola:
● Se [tex]a\gt 0[/tex]:
a função quadrática é crescente no intervalo [tex]\left\{x \in \mathbb{R}~|~x \geqslant x_v \right\}[/tex]
a função quadrática é decrescente no intervalo [tex]\left\{x \in \mathbb{R}~|~x \leqslant x_v \right\}[/tex]
● Se [tex]a\lt 0[/tex]:
a função quadrática é crescente no intervalo [tex]\left\{x \in \mathbb{R}~|~x \leqslant x_v \right\}[/tex]
a função quadrática é decrescente no intervalo [tex]\left\{x \in \mathbb{R}~|~x \geqslant x_v \right\}[/tex]

Função Modular
Antes de definirmos função modular, vamos relembrar o que é o módulo de um número real.
Dado um número real [tex]x[/tex], chama-se módulo ou valor absoluto de [tex]x[/tex] (indica-se por [tex]|x|[/tex]), o número real não negativo tal que
[tex]\qquad \qquad |x| = \begin{cases}x, \text{ se } x\geq 0\\
-x, \text{ se } x\lt 0\end{cases}.[/tex]
Assim, a função modular pode ser definida como uma função [tex]f[/tex] de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex] tal que:
[tex]\qquad f(x)= \begin{cases}x, \text{ se } x\geq 0\\
-x, \text{ se } x\lt 0\end{cases}.[/tex]
Analisando a lei de formação composta da função modular, podemos concluir que o gráfico da função [tex]f(x) = |x|[/tex] é formado por duas semirretas com origem na origem do plano cartesiano e seguindo um formato de “V”, conforme figura abaixo.

Observando o gráfico da função modular definida de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex], podemos concluir que:
● A função modular não é sobrejetora.
● A função modular não é injetora.
● A função modular não é crescente.
● A função modular não é decrescente.
Além da função modular, podemos definir outras funções envolvendo módulo.
Vejamos dois exemplos.
[tex]\qquad f(x) = |x-2| = \begin{cases}x-2, \text{ se } x-2\geq 0\\
-(x-2), \text{ se } x-2\lt 0\end{cases}\\
\qquad f(x) = \begin{cases}x-2, \text{ se } x\geq 2\\
-x+2, \text{ se } x\lt 2\end{cases}\\
~~[/tex]
e, assim, o gráfico da função [tex]f[/tex] é formado pelas duas semirretas:
[tex]\qquad \boxed{y=x-2}[/tex], se [tex]x\geq 2[/tex];
e
[tex]\qquad \boxed{y=-x+2}[/tex], se [tex]x\lt 2[/tex].

Exemplo 2: Dada a função modular [tex]g:\mathbb{R}\rightarrow \mathbb{R}[/tex] definida por [tex]g(x) = |x|-1[/tex], temos
[tex]\qquad |x| = \begin{cases}x, \text{ se } x\geq 0\\
-x, \text{ se } x\lt 0\end{cases}. [/tex]
Portanto,
[tex]\qquad |x|-1 = \begin{cases}x-1, \text{ se } x\geq 0\\
-x-1, \text{ se } x\lt 0\end{cases}.[/tex]
Assim, o gráfico da função é formado pelas duas semirretas:
[tex]\qquad \boxed{y=x-1}[/tex], se [tex]x\geq 0[/tex];
e
[tex]\qquad\boxed{y=-x-1}[/tex], se [tex]x\lt 0[/tex].

Função Exponencial
A função exponencial possui diversas aplicações práticas, sendo usada para modelar, por exemplo, o crescimento de populações de animais, taxas de juros compostos em investimentos financeiros, o aumento da temperatura média global ao longo do tempo, entre outros.
Vamos iniciar o nosso estudo de funções exponenciais a partir de um problema prático: Considere que um investimento cresce a uma taxa de juros compostos de [tex]6\;\%[/tex] ao ano. Se você investir [tex]R$\, 1\;000,00[/tex] hoje, quanto terá depois de [tex]t[/tex] anos?
O montante do investimento após [tex]t[/tex] anos é dado por [tex]M(t) = C\cdot (1 + i)^t,[/tex] sendo [tex]C[/tex] o capital investido, [tex]i[/tex] a taxa de juros e [tex]t[/tex] o tempo decorrido. Substituindo os valores dados, temos
[tex]\qquad M(t) = 1\;000\cdot (1 + 0,06)^t = 1\;000\cdot (1,06)^t.[/tex]
Portanto, o montante total depois de [tex]t[/tex] anos é dado por [tex]1\;000\cdot (1,06)^t[/tex] reais.
São exemplos de funções exponenciais as funções [tex]f,~g,~h,~p: \mathbb{R}\longrightarrow \mathbb{R}_+^*[/tex] dadas por:
[tex]\qquad f(x) = 2^x[/tex];
[tex]\qquad g(x) = \left(\dfrac{1}{3}\right)^x[/tex];
[tex]\qquad h(x) = (\sqrt{5})^x[/tex];
[tex]\qquad p(x) = \pi^x.\\[/tex]
Uma outra função exponencial bastante conhecida é a chamada função exponencial natural , [tex]q(x) = e^x[/tex], para a qual a base é o número de Euler [tex]e[/tex] (número irracional cujo valor é de aproximadamente [tex]2,71[/tex]).
Algumas observações devem ser destacadas com relação a uma função exponencial:
► Como na definição de função exponencial devemos ter [tex]a\gt 0[/tex], então independentemente do valor de [tex]x[/tex], teremos sempre [tex]a^x\gt 0[/tex], ou seja, [tex]f(x)\gt 0[/tex] e, assim, o gráfico de [tex]f[/tex] nunca intersecta o eixo [tex]x.\\[/tex]
► Para uma função exponencial qualquer [tex]f(x) = a^x[/tex], temos [tex]f(0) = a^0 = 1[/tex], o que implica que o gráfico sempre intersecta o eixo [tex]y[/tex] em [tex]y = 1.\\[/tex]
► A função exponencial [tex]f(x) = a^x[/tex] é decrescente se, e somente se, [tex]0\lt a\lt 1.[/tex]
Solução: Como no exemplo temos [tex]a = \dfrac{1}{3}[/tex], e [tex]0\lt \dfrac{1}{3}\lt 1[/tex], então a função [tex]f[/tex] de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex] dada por [tex]f(y) = \left(\dfrac{1}{3}\right)^y[/tex] é decrescente; com isso, quanto maior for [tex]y[/tex], menor será o valor de [tex]f(y)[/tex]. Assim, precisamos encontrar o valor de [tex]x[/tex] que torna o expoente [tex]4x-x^2[/tex] maior possível.
Definindo a função [tex]g[/tex] de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex] dada por [tex]g(x) = 4x-x^2[/tex], vemos que [tex]g[/tex] é função quadrática com concavidade para baixo, então o máximo é atingido em
[tex]\qquad y_v = -\dfrac{b^2-4ac}{4a} = -\dfrac{4^2-4\cdot (-1)\cdot 0}{4\cdot (-1)} = 4[/tex].
Logo, o menor valor da expressão, é [tex]\left(\dfrac{1}{3}\right)^4 = \dfrac{1}{81}[/tex].
O comportamento do gráfico da função exponencial [tex]f(x)=a^x[/tex] depende unicamente do valor que [tex]a[/tex] assume:
► se [tex]a\gt 1[/tex], a função é crescente e o gráfico tem o seguinte comportamento:

► se [tex]0\lt a\lt 1[/tex], a função é decrescente e o gráfico tem a seguinte forma:

Equipe COM – OBMEP
