Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Fácil)
Uma carta foi retirada de um baralho completo.
Qual a probabilidade de essa carta ser um Rei ou uma carta de Ouros?
Solução
Uma carta foi retirada de um baralho completo ([tex]52[/tex] cartas) e queremos calcular a probabilidade de essa carta ser "um Rei" ou "uma carta de Ouros".
Observe que o espaço amostral do problema é
- [tex]\Omega[/tex]: "todas as cartas do baralho"
e estão envolvidos dois eventos:
- evento [tex]\textcolor{#52D017}{E_1}[/tex]: a carta retirada ser um "Rei";
- evento [tex]\textcolor{red}{E_2}[/tex]: a carta retirada ser do naipe "Ouros".
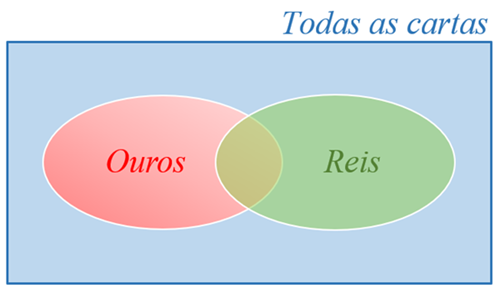
Se [tex]P(X)[/tex] indicar a probabilidade de um evento [tex]X[/tex], o que precisaremos calcular é [tex]P(E_1 \cup E_2)[/tex] e para isso utilizaremos a fórmula:
[tex]\qquad \qquad \boxed{P(E_1 \cup E_2)= \textcolor{#52D017}{P(E_1)}+\textcolor{red}{P(E_2)}-P(E_1 \cap E_2)}[/tex],
ou seja, "a probabilidade de a carta retirada ser de Ouros ou um Rei" é "a probabilidade de a carta ser de Ouros", mais "a probabilidade de a carta ser um Rei", menos "a probabilidade de a carta ser um Rei de Ouros".
Vamos, então, calcular separadamente [tex]\textcolor{#52D017}{P(E_1)}[/tex], [tex]\textcolor{red}{P(E_2)}[/tex] e [tex]P(E_1 \cap E_2):[/tex]
- Para tirarmos um Rei, dispomos de [tex]4[/tex] de um total de [tex]52[/tex] cartas.
Assim, [tex]\boxed{\textcolor{#52D017}{P(E_1)=\dfrac{4}{52}=\dfrac{1}{13}}} \, .[/tex] - Para tirarmos uma carta de Ouros, dispomos de [tex]13[/tex] de um total de [tex]52[/tex] cartas.
Assim, [tex]\boxed{\textcolor{red}{P(E_2)=\dfrac{13}{52}=\dfrac{1}{4}}} \, .[/tex] - Para tirarmos um Rei de Ouros, dispomos de [tex]1[/tex] carta de um total de [tex]52[/tex] cartas.
Assim, [tex]\boxed{P(E_1\cap E_2)=\dfrac{1}{52}} \, .[/tex]
Dessa forma, segue que:
[tex]\qquad \qquad P(E_1 \cup E_2)= \textcolor{#52D017}{P(E_1)}+\textcolor{red}{P(E_2)}-P(E_1 \cap E_2)[/tex]
[tex]\qquad \qquad P(E_1 \cup E_2)= \textcolor{#52D017}{\dfrac{1}{13}}+\textcolor{red}{\dfrac{1}{4}}-\dfrac{1}{52}\\
\, \, [/tex]
[tex]\qquad \qquad P(E_1 \cup E_2)=\dfrac{16}{52}=\dfrac{4}{13}.[/tex]
Portanto, a probabilidade de que a carta retirada seja um Rei ou uma carta de Ouros é [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{4}{13}$} \, [/tex], ou seja, aproximadamente [tex] \, \fcolorbox{black}{#eee0e5}{$31\%$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
