Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
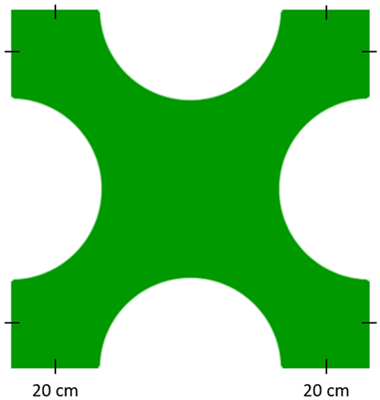
A família Xiis precisa de um logotipo para a placa que será colocada na fachada de sua loja. O filho mais novo fez o desenho abaixo, a partir de um quadrado de lados medindo 80 cm e de quatro semicírculos, mas precisa comprar tinta para pintá-lo.
Qual a medida aproximada da área do logotipo que será pintada de verde?
Solução
A partir das informações e da figura fornecidas pelo problema, podemos concluir que a área verde do logotipo é a diferença entre a "área de um quadrado de lados [tex]80\,cm[/tex]" e a " soma das áreas de quatro semicírculos de raio [tex]20\,cm[/tex]".
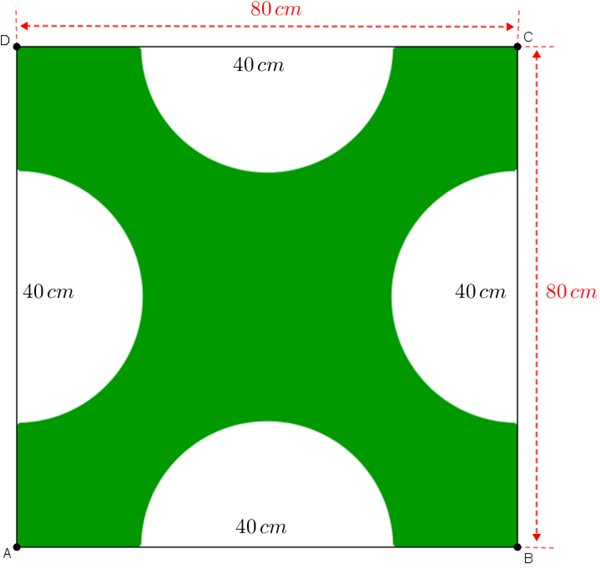
- A área de um quadrado de lados [tex]80\,cm[/tex] é [tex]\boxed{A_q=80^2=6400\, cm^2} \, .[/tex]
- A área de um semicírculo de raio [tex]20\,cm[/tex] é [tex]\boxed{A_{sc}=\dfrac{\pi\,20^2}{2}=200\pi\, cm^2} \, .[/tex]
Assim, se [tex]\textcolor{#2fbf2f}{A_{verde}}[/tex] é a área verde do logotipo, então:
[tex]\qquad \textcolor{#2fbf2f}{A_{verde}}=A_q-4\times A_{sc} [/tex]
[tex]\qquad \textcolor{#2fbf2f}{A_{verde}}=6400-4 \times 200\pi [/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$\textcolor{#2fbf2f}{A_{verde}}=(6400-800\pi)\, cm^2 \approx 3888 \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
