Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. M.- Nível de dificuldade: Médio)
(Adaptado de Construindo conhecimento em Matemática, 8ª série – Bianchini; Miani; Editora Moderna, 2000) As medidas do triângulo de carro que é mostrado na figura estão expressas em centímetros.
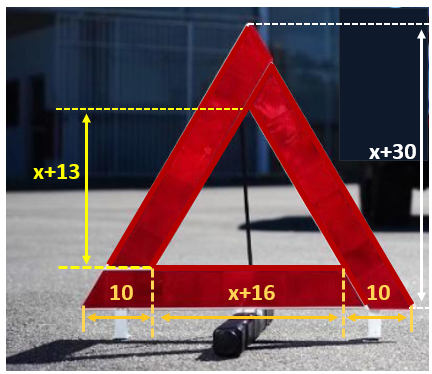
Determine uma expressão algébrica que representa a área vermelha que vemos na figura.
Solução
Observando a figura, vemos que a área vermelha, [tex]\textcolor{red}{A_{verm}}[/tex], é a diferença entre a área do triângulo maior (triângulo externo) e a área do triângulo menor (triângulo interno).
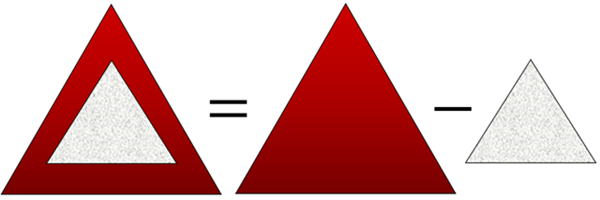
Vamos então calcular a área desses dois triângulos. Denotaremos por [tex]A_T\, [/tex] e [tex]\; A_t[/tex] as áreas do triângulo maior e do triângulo menor, respectivamente.
[tex]\quad A_T=\dfrac{\left(10+x+16+10\right)\cdot \left(x+30\right)}{2}\\
\quad A_T=\dfrac{\left(36+x\right)\cdot \left(x+30\right)}{2}\, \text{cm}^2.[/tex]
[tex]\quad A_t=\dfrac{\left(x+16\right)\cdot \left(x+13\right)}{2}\, \text{cm}^2.[/tex]
Assim, segue que:
[tex]\quad \textcolor{red}{A_{verm}}=[/tex] área do triângulo maior – área do triângulo menor
[tex]\quad \textcolor{red}{A_{verm}}=A_T-A_t\\
\quad \textcolor{red}{A_{verm}}=\dfrac{\left(36+x\right)\cdot \left(x+30\right)}{2}-\dfrac{\left(x+16\right)\cdot \left(x+13\right)}{2}\\
\quad \textcolor{red}{A_{verm}}=\dfrac{\left(36x+1080+x^2+30x\right)-\left(x^2+13x+16x+208\right)}{2}\\
\quad \textcolor{red}{A_{verm}}=\dfrac{36x+1080+x^2+30x-x^2-13x-16x-208}{2}\\
\quad \textcolor{red}{A_{verm}}=\dfrac{37x-872}{2}.[/tex]
Portanto, uma expressão algébrica que representa a área vermelha em [tex]cm^2[/tex] é [tex]\;\fcolorbox{black}{#eee0e5}{$\,\dfrac{37x-872}{2}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
