Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
Jorginho desenhou um icoságono regular e nomeou um de seus vértices de [tex]A[/tex]. Em seguida, traçou todas as diagonais desse polígono, exceto aquelas que têm [tex]A[/tex] como vértice.
Quantas foram as diagonais que Jorginho traçou?
Solução
Lembramos que um icoságono regular é um polígono com vinte vértices e vinte lados de mesmo comprimento. Assim, como as diagonais de um polígono são segmentos definidos por dois de seus vértices distintos e não consecutivos (observe que dois vértices consecutivos definem um lado e não uma diagonal de um polígono), então de cada vértice saem [tex]\boxed{20-3=17}[/tex] diagonais.
Como o icoságono tem vinte vértices, a princípio teríamos [tex]20 \times 17=340[/tex] diagonais. Mas perceba que nessa contagem cada diagonal está sendo contada duas vezes (a diagonal do vértice [tex]A [/tex] ao vértice [tex] V_{10} [/tex], por exemplo, é a mesma do vértice [tex]V_{10} [/tex] ao vértice [tex]A [/tex]); portanto, o número de diagonais do icoságono desenhado pelo Jorginho é [tex]\dfrac{340}{2}=170.[/tex]
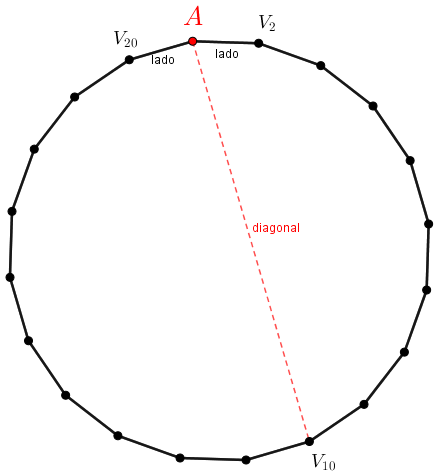
Observe que, dessas [tex]170[/tex] diagonais, [tex]\boxed{20-3=17}[/tex] têm o ponto [tex]A [/tex] como extremidade; assim, Jorginho traçou [tex] \, \fcolorbox{black}{#eee0e5}{$170-17=153$} \, [/tex] diagonais.
|
De modo geral, o raciocínio que fizemos para determinar o número de diagonais de um polígono regular de [tex]17[/tex] lados pode ser utilizado para se obter o número de diagonais de um polígono regular com um número qualquer de lados. |
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
