Clique no botão abaixo para visualizar o problema.
Problema
No triângulo retângulo [tex]ABC[/tex] mostrado abaixo, [tex]BD = CD[/tex].
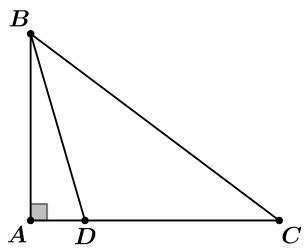
Sabendo que [tex]AB = 3[/tex] e [tex]AC = 4[/tex], determine o valor de [tex]CD[/tex].
Solução 1
Denotemos por [tex]x[/tex] a medida [tex]CD[/tex], então [tex]BD = x[/tex] e, como [tex]AC = 4[/tex], temos [tex]AD = AC-CD = 4-x[/tex], conforme indicado na figura abaixo.
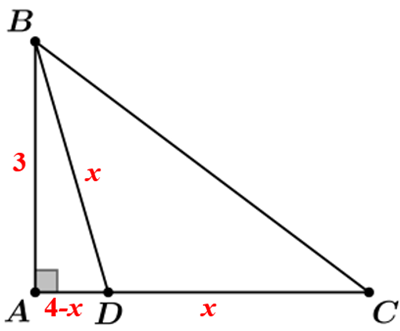
Aplicado o Teorema de Pitágoras ao triângulo [tex]ABD[/tex], temos:
[tex]\qquad x^2 = 3^2+(4-x)^2[/tex]
[tex]\qquad x^2 = 3^2+4^2-8x+x^2[/tex]
[tex]\qquad 8x = 9+16[/tex]
[tex]\qquad 8x = 25[/tex]
[tex]\qquad x = \dfrac{25}{8} = 3,125.[/tex]
Portanto, [tex]\fcolorbox{black}{#eee0e5}{$CD=3,125$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Primeiramente, focando no triângulo retângulo [tex]ABD[/tex], podemos aplicar o teorema de Pitágoras para obtermos o seguinte:
[tex]\qquad (BD)^2 = (AB)^2 + (AD)^2.\qquad \textcolor{#800000}{(i)}[/tex]
Analisando o triângulo [tex]ABC[/tex], observamos que [tex]\boxed{AD = AC-DC}.[/tex]
Substituindo essa igualdade em [tex]\textcolor{#800000}{(i)}[/tex] e desenvolvendo, ficamos com:
[tex]\qquad (BD)^2 = (AB)^2 + (AC – DC)^2\\
\qquad (BD)^2 = (AB)^2 + (AC)^2-2 \cdot (AC) \cdot (DC) + (DC)^2.\qquad \textcolor{#800000}{(ii)}\\
~~[/tex]
Como [tex]BD = DC[/tex], então [tex]BD^2 = DC^2[/tex]; assim, podemos simplificar estes termos em [tex]\textcolor{#800000}{(ii)}[/tex]:
[tex]\qquad 0 = (AB)^2 + (AC)^2 – 2 \cdot (AC) \cdot (DC)\\
~~[/tex]
Agora, aplicando os valores numéricos para [tex]AB[/tex] e [tex]AC[/tex], obtemos:
[tex]\qquad 0 = 3^2 + 4^2-2 \cdot 4 \cdot (DC)\\
\qquad 0 = 9 + 16-8 \cdot (DC)\\
\qquad 0 = 25-8(DC)\\
\qquad 8(DC) = 25\\
\qquad DC = \dfrac{25}{8}.[/tex]
Assim, concluímos que o valor de [tex]CD[/tex] é [tex]\,\fcolorbox{black}{#eee0e5}{$\dfrac{25}{8}=3,125$}\,.[/tex]
Solução elaborada pelo COM Potências de Euler.
Nível A – Questão Mediana
