(A) Problema de Gincana: Um retângulo aumentado

Clique no botão abaixo para visualizar o problema.

Problema

Se aumentássemos

$5\text{ cm}$ no comprimento e

$5\text{ cm}$ na largura de um retângulo R, a sua área aumentaria de

$155\text{ cm}^2.$
Qual o perímetro desse retângulo R, em centímetros?

(Adaptado da III ONEM.)

Solução

Vamos denotar por

$a~$ e

$~b$ a altura e a base, respectivamente, do retângulo R.
A figura a seguir mostra o retângulo inicial e, depois, com as dimensões aumentadas; representamos a área de R por

$A.$

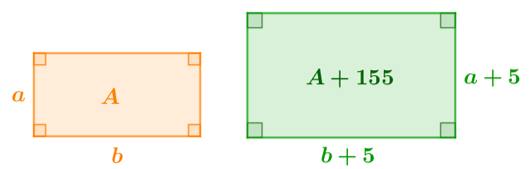
Observando as duas imagens, concluímos, de imediato, que $\boxed{A=a\cdot b}~$ e $~\boxed{A+155=(a+5)\cdot (b+5)}.$
Dessa forma, segue que:
$\qquad A+155=(a+5)\cdot (b+5)\\ \qquad a\cdot b+155=(a+5)\cdot (b+5)\\ \qquad a\cdot b+155= a\cdot b+5\cdot a+5\cdot b+25\\ \qquad \cancel{a\cdot b}+155= \cancel{a\cdot b}+5\cdot a+5\cdot b+25\\ \qquad 155= 5\cdot a+5\cdot b+25\\ \qquad 130= 5\cdot (a+b)\\ \qquad a+b=26.\\$
Como o perímetro $P$ do retângulo inicial R é $P=2\cdot a+2\cdot b$ , segue que:
$\qquad P=2\cdot (a+b)\\ \qquad P=2\cdot 26=52.\\$
Portanto, o perímetro do retângulo R é $\fcolorbox{black}{#FFE3AA}{$52 \text{ cm}$}\,.$

Solução elaborada pelos Moderadores do Blog.

Primeira Gincana de 2023 – Clubes de Matemática da OBMEP
Nível A – Questão Mediana