Clique no botão abaixo para visualizar o problema.
Problema
Franci elaborou uma lista contendo todos os números de quatro dígitos formados pelos algarismos 0, 1, 2 e 3.
(Por exemplo, 1023 e 2122 estão nessa lista, mas 0123 não, pois é considerado um número de três dígitos.)
Qual é a soma de todos os números dessa lista?
Solução
Inicialmente, observe que:
- Em um número qualquer dessa lista, o primeiro dígito pode ser qualquer um dos três algarismos: [tex]1[/tex], [tex]2[/tex] ou [tex]3.[/tex]
- Já os demais dígitos podem ser qualquer um dos quatro algarismos: [tex]0[/tex], [tex]1[/tex], [tex]2[/tex] ou [tex]3.[/tex]
Assim, o total de elementos da lista é [tex]3\times 4\times 4\times 4 = 192[/tex] elementos.
Observe, agora, que o total de números em que o [tex]0[/tex] aparece na unidade é igual ao total de números em que o [tex]1[/tex] aparece, bem como o [tex]2[/tex] e o [tex]3. [/tex] O mesmo acontecendo com a quantidade de vezes que cada um desses quatro algarismos aparece na casa das dezenas e na casa das centenas.
Portanto, [tex]192\div 4 = 48[/tex] números têm o [tex]0[/tex] na casa das unidades, [tex]48[/tex] têm o [tex]1[/tex] na casa das unidades, [tex]48[/tex] têm o [tex]2[/tex] na casa das unidades e [tex]48[/tex] têm o [tex]3[/tex] na cada das unidades.
Analogamente, cada um dos dígitos [tex]0[/tex], [tex]1[/tex], [tex]2[/tex] e [tex]3[/tex] aparece em [tex]48[/tex] números na casa das dezenas e em [tex]48[/tex] números na casa das centenas.
Agora, o total de números em que o [tex]1[/tex], o [tex]2[/tex] ou o [tex]3[/tex] aparece na unidade de milhar são [tex]192\div 3 = 64[/tex] números, pois nenhum dos números pode começar com [tex]0.[/tex]
Finalmente, se dispormos todos os [tex]192[/tex] números numa lista para somá-los, percebam que:
(i) a soma dos algarismos nas casas das unidades de todos eles será [tex](0+1+2+3)\times 48=288.[/tex] No esqueminha da soma, ficam [tex]\textcolor{red}{8}[/tex] unidades na casa das unidades e vão [tex]\textcolor{red}{28}[/tex] para a coluna das dezenas;
(ii) a soma dos algarismos nas casas das dezenas também será [tex](0+1+2+3)\times 48=288[/tex]; mas, com os [tex]28[/tex], teremos [tex]288+28=316.[/tex] No esqueminha da soma, ficam [tex]\textcolor{blue}{6}[/tex] unidades na casa das dezenas e vão [tex]\textcolor{blue}{31}[/tex] para a coluna das centenas;
(iii) a soma dos algarismos nas casas das centenas também será [tex] 288[/tex]; com os [tex]31[/tex], teremos [tex]288+31=319.[/tex] No esqueminha da soma, ficam [tex]\textcolor{#FF00FF}{9}[/tex] unidades na casa das dezenas e vão [tex]\textcolor{#FF00FF}{31}[/tex] para a coluna dos milhares;
(iv) a soma dos algarismos nas casas dos milhares será [tex](1+2+3)\times 64=384[/tex]; com os [tex]31[/tex], teremos [tex]384+31=415[/tex] e terminamos a soma!
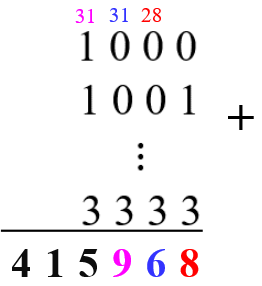
Logo, a soma de todos os elementos da lista é [tex] \fcolorbox{black}{#FFE3AA}{$415\; 968$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Nível A – Questão Difícil
