(A) Problema: Cercando a propriedade

Clique no botão abaixo para visualizar o problema.

Problema
(Indicado a partir do 6º ano do E. F.)

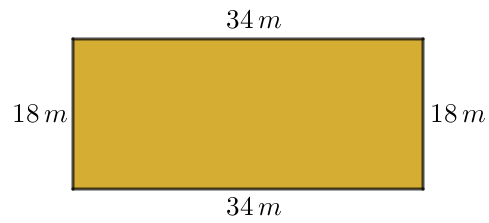
(IFPE, 2019 – Adaptado) O Sr. Leôncio comprou um terreno retangular que mede

$18$ metros de largura por

$34$ metros de comprimento. Para cercar completamente sua propriedade, ele comprou estacas de madeira e rolos de arame farpado. A pessoa contratada para fazer o serviço sugeriu que fosse feita uma cerca de modo que fossem dadas cinco voltas de arame contornando todo o perímetro, conforme mostra a figura abaixo.

Leôncio acatou a sugestão.
Sabendo que o arame farpado é vendido em rolos de $60$ metros, determine quantos rolos, no mínimo, serão comprados.

Solução

O perímetro do terreno é de

$2\cdot (18+34) = 104 \text{ m}.$

Assim, o comprimento de arame farpado que será utilizado é igual a

$104\times 5 = 520 \text{ m}.$
Como o arame é vendido em rolos de

$60$ metros, vamos dividir

$520$ por

$60$ para determinarmos a quantidade de rolos de arame que deverão ser comprados:

$\qquad \qquad \begin{array}{r} 520 \, \end{array} \begin{array}{|r} \, 60 \, \, \, \\ \hline \end{array}$

$\qquad \qquad\begin{array}{r} \;40 \end{array}\begin{array}{r} \quad \, 8 \end{array}\qquad \qquad$

Como $520=60\times 8+40$ , deverão ser comprados $9$ rolos e ainda sobrará $9\times 60-520 = 20 \text{ m}$ de arame.

Solução elaborada pelos Moderadores do Blog.