Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir da 1ª série do E. M.)
No plano cartesiano da figura abaixo, no qual os eixos estão graduados em quilômetros, estão representados os gráficos da função
f:[0,52]→R, definida por f(x)=−12x2+52x,
e da função afim
g:[52,5]→R, cujo coeficiente angular é −54.
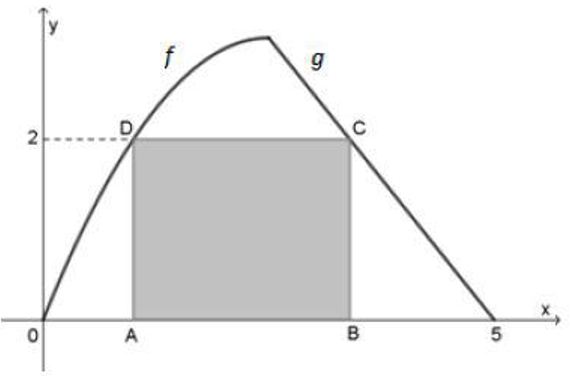
O retângulo ABCD tem os vértices A e B sobre o eixo das abscissas e os vértices C e D sobre os gráficos das funções g e f respectivamente, e ambos possuem ordenadas iguais a 2.
Qual é a medida da área desse retângulo, em quilômetros quadrados?
Extraído de PISM I.
Solução
A área de um retângulo é calculada pela multiplicação da medida da base pela medida da altura. Pelo enunciado, concluímos que a altura possui medida 2 km.
Ao fazermos f(x)=2, encontramos:
f(x)=2−12x2+52x=2−x2+5x=4x2−5x+4=0.
Podemos resolver essa última equação do 2º grau utilizando a sua fórmula resolutiva:
x=−b±√b2−4ac2ax=5±√25−162x=5±32x=82=4 ou x=22=1.
Como o domínio da f é o intervalo [0,52], temos como única opção x=1.
Portanto, o ponto A tem coordenadas A=(1,0).
Como o gráfico da função g é um segmento de reta que possui coeficiente angular igual a −54, podemos escrever a lei de formação de g da seguinte maneira:
g(x)=−54x+b.
Observando o gráfico, vemos que g(5)=0; assim, segue que:
−54⋅5+b=0b=254
e, portanto, a função g possui a seguinte lei de formação: g(x)=−54x+254.
Agora, para descobrirmos o valor da abcissa do ponto B, basta fazermos g(x)=2. Observe:
g(x)=2−54x+254=2−5x+25=8x=175.
Com isso, B=(175,0).
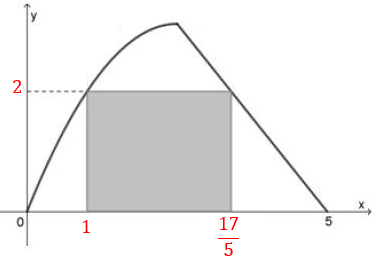
Dessa forma, temos que a medida da base do retângulo ABCD é dada por:
175−1=125=2,4 km.
Logo, a área desse retângulo mede 2,4×2=4,8 km2 .
Solução elaborada pelos Moderadores do Blog.
