A Matemática do vídeo Inspirations – Tema 3

A cicloide, que aparece perto dos 50 segundos do vídeo, é a curva descrita por um ponto P na circunferência de um círculo quando este se movimenta ao longo de uma linha reta.
Por exemplo, se sobre o lado de uma roda de um carro ou de uma bicicleta marca-se um ponto com giz, a curva descrita (trajetória) por esse ponto quando o carro ou a bicicleta estiver em movimento é uma cicloide. Esta é uma das mais famosas curvas da história da matemática e tem uma série de propriedades curiosas.

Uma das primeiras pessoas a estudar a cicloide foi Galileu, que propôs que pontes poderiam ser construídas no formato de cicloides e que tentou encontrar a área sob um arco de uma cicloide.

Mas foi no século XVII que a cicloide recebeu a atenção de nomes famosos como Descartes, Mersenne, Pascal, Galileu,Torricelli e Roberval. Nessa época foi possível, por exemplo, calcular a área por ela delimitada, traçar sua tangente por um ponto qualquer, determinar o comprimento de um arco ligando dois pontos arbitrários.

Conta-se que, numa noite em que sofria de uma dor de dentes, o matemático francês Blaise Pascal (1623-1662) começou a pensar na cicloide e quando se apercebeu a dor de dentes já tinha desaparecido. Ele tomou isto como um sinal de Deus, e estudou a cicloide mais profundamente. Pascal descobriu certas áreas, volumes e centros de gravidade associados à cicloide.
 
 

Tautocronismo e Braquistócrona

• O físico holandês Christian Huygens (1629-1695) provou que um ponto material, partindo do repouso e deixado deslizar sem atrito sobre um arco de cicloide invertido, atinge o nível inferior em um intervalo de tempo que independe do ponto de partida. A esta propriedade deu-se o nome de tautocronismo, do grego tauto, que significa igual, e cronos, que significa tempo.

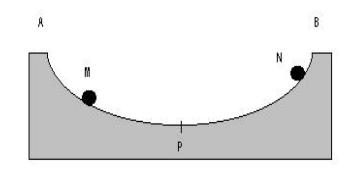
Imagine uma cicloide virada para cima e que deixemos cair por ela, a partir dos pontos M e N, duas bolinhas de gude. O que irá acontecer?
Por mais incrível pareça, as bolinhas chegam ao mesmo tempo ao ponto mais baixo da cicloide, independentemente do comprimento do caminho que cada uma percorre.

• O matemático suíço Johann Bernoulli, foi quem apresentou, em 1696, o problema da Braquistócrona: encontrar a trajetória que minimiza o tempo gasto por um corpo, partindo do repouso e sujeito apenas à ação da gravidade, para ir de um ponto a outro, em níveis diferentes e não situados sobre a mesma vertical. Johann Bernoulli mostrou que dentre todas as possíveis curvas que unem os pontos A e B, uma partícula levará o menor tempo deslizando de A até B se a curva for um arco invertido de uma cicloide. O Problema da Braquistócrona também foi resolvido por Jakob Bernoulli (irmão de Johann Bernoulli), por Isaac Newton, por Gottfried Leibniz e pelo Marquês de L´Hospital.

Diz-se, embora sem comprovação, que Newton soube do problema da Braquistócrona no final da tarde de um dia cansativo de trabalho na Casa da Moeda da Inglaterra e que o resolveu naquela noite, após o jantar. Ele teria publicado a solução anonimamente no jornal da Royal Society; mas, tempos depois, ao ler a solução publicada Johann Bernoulli observou: – “Ah, conheço o leão pela sua pata.”

Jonas Cassiano Costa e Roger Leite Lucena
alunos do PIC – OBMEP
Clubes Os Geométricos e Os Modulares