Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 2º ano do E. M.)
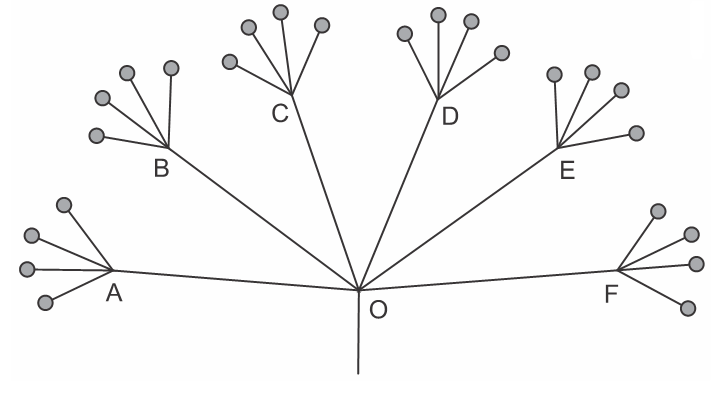
(Fuvest, 2021) Um parque industrial com [tex]24[/tex] indústrias foi estruturado de forma que seu sistema de esgoto tivesse a estrutura mostrada na figura. Um serviço de inspeção no ponto [tex]O[/tex] detectou uma substância proibida que pode ter vindo de qualquer uma das indústrias, com igual probabilidade. Para autuar as indústrias irregulares, o serviço decidiu pela seguinte estratégia: usar [tex]6[/tex] kits de teste em amostras coletadas nos pontos [tex]A, B, C, D, E[/tex] e [tex]F[/tex], no primeiro dia e, no segundo dia, fazer o mesmo nas saídas de todas as indústrias dos grupos apontados como contaminados no primeiro dia.
a) Quantas são as formas possíveis de exatamente quatro indústrias irregulares estarem distribuídas entre as [tex]24[/tex] indústrias do parque?
b) Havendo exatamente quatro indústrias irregulares, qual é a probabilidade de que o gasto total de kits de testes nos dois dias seja [tex]22[/tex]?
c) Qual é a probabilidade, havendo exatamente quatro indústrias irregulares, de que o gasto total de kits de testes usados nos dois dias seja [tex]14[/tex] ou menos?

Ajuda
✏ A probabilidade de um evento ocorrer em um modelo com espaço amostral finito e equiprovável é calculada por:
| Probabilidade[tex]\;\;[/tex] = | número de casos favoráveis | . |
| número de casos possíveis |
✏ Uma das maneiras de agruparmos elementos de um dado conjunto é escolhê-los levando-se em consideração apenas a sua natureza, sem se importar em que ordem eles foram escolhidos ou apresentados. Esse tipo de agrupamento de elementos é denominado uma Combinação simples. Especificamente, quando escolhemos [tex]r[/tex] dentre [tex]n[/tex] elementos de um conjunto dessa forma, dizemos que estamos definindo uma Combinação simples de [tex]n[/tex] elementos tomados [tex]r[/tex] a [tex]r[/tex].
E o legal é que, dado um conjunto finito, podemos determinar quantos agrupamentos desse tipo podemos fazer, sem que precisemos exibi-los.
- O número de Combinações simples de [tex]n[/tex] elementos, tomados [tex]r[/tex] a [tex]r[/tex], é denotado por [tex]C_{n\, ,\, r}[/tex] ou [tex]C_n^r[/tex] e assim definido:
[tex]C_{n\, ,\, r}=C_n^r=\dfrac{n!}{(n-r)!\, r!} \text{, com } n,r \in\mathbb{N} \text{ e }\,0 \lt r\leqslant n[/tex].
O quociente [tex]\dfrac{n!}{(n-r)!\, r!}[/tex] também pode ser denotado por [tex]\dbinom{n}{r}[/tex] e nesse caso é denominado coeficiente binomial ou número binomial.
✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo: Se
- uma escolha E1 puder ser feita de [tex] m_1 [/tex] maneiras distintas,
- uma escolha E2 puder ser feita de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma escolha Ek puder ser feita de [tex]m_k [/tex] maneiras distintas e
- todas essas escolhas forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),
então o número total de maneiras de serem feitas sucessivamente essas [tex]k[/tex] escolhas é igual ao produto
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k} \, .[/tex]
Solução
a) Como qualquer uma das indústrias pode ser irregular, o total de formas possíveis de quatro indústrias estarem irregulares é
[tex]\qquad C_{24,4} = \dfrac{24!}{4!(24-4)!} = \dfrac{24\cdot 23\cdot 22\cdot 21}{4!} = 10\;626.[/tex]
b) Como no primeiro dia são usados exatamente [tex]6[/tex] kits de testes, então no segundo devem ter sido usados [tex]22-6 = 16[/tex] kits de testes. Juntando esta informação com o fato de que há [tex]4[/tex] indústrias irregulares, conclui-se que no segundo dia foram testados apenas [tex]4[/tex] grupos, com uma indústria irregular por grupo.
Como em cada grupo a indústria irregular pode ser qualquer uma das quatro, o total de formas possíveis de ocorrência dessa situação é
[tex]\qquad C_{6,4}\cdot 4\cdot 4\cdot 4\cdot 4 = 15\cdot 4\cdot 4\cdot 4\cdot 4 = 3840.[/tex]
Assim, a probabilidade procurada é [tex]\dfrac{3840}{10\;626} = \dfrac{640}{1771}[/tex], ou seja, aproximadamente [tex]36\%.[/tex]
c) Como no primeiro dia são usados exatamente [tex]6[/tex] kits de testes, então o total de kits que devem ter sido gastos no segundo dia é [tex]14-6 = 8[/tex] ou menos. Assim, as [tex]4[/tex] indústrias devem estar distribuídas em no máximo dois grupos, caso contrário, precisariam ter sido gastos pelo menos [tex]12[/tex] testes no segundo dia. Analisaremos então o problema por casos.
- 1) As quatro indústrias irregulares estão em um único grupo:
O total de maneiras de acontecer essa situação é [tex]6[/tex], uma vez que as indústrias irregulares podem estar em qualquer um dos seis grupos.
- 2) Existem dois grupos com duas indústrias irregulares em cada um:
Como existem [tex]C_{6,2}[/tex] formas de definir os dois grupos e para cada uma dessas formas existem [tex]C_{4,2}[/tex] maneiras de existirem duas indústrias irregulares em cada grupo, então o total de maneiras de acontecer a situação deste caso é
[tex]\qquad C_{6,2}\cdot C_{4,2}\cdot C_{4,2} = 15\cdot 6\cdot 6 = 540.[/tex]
- 3) Existem três indústrias irregulares em um grupo e uma em outro grupo:
Observe que existem [tex]C_{6,2}[/tex] formas de definir os dois grupos e, definidos os grupos, existem duas maneiras de definir em qual grupo estão as três indústrias irregulares. Além disso, para cada uma dessas maneiras existem [tex]C_{4,3}[/tex] formas de existirem três indústrias irregulares no determinado grupo e [tex]4[/tex] formas de existir uma indústria irregular no outro grupo. Logo, o total de maneiras de acontecer a situação deste caso é
[tex]\qquad 2\cdot C_{6,2}\cdot C_{4,3}\cdot 4 = 2\cdot 15\cdot 4\cdot 4 = 480.[/tex]
Portanto, a probabilidade pedida é [tex]\dfrac{6+540+480}{10\;626} = \dfrac{171}{1\;771}[/tex], aproximadamente [tex]9,7\%.[/tex]
Solução elaborada pelos Moderadores do Blog.
