A álgebra das funções reais
… e um pouco mais
Vamos recordar algumas definições que permitirão definir uma estrutura matemática para o conjunto das funções de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex], conjunto este que passaremos a denotar por [tex]\mathbb{R}^{\mathbb{R}}[/tex]:
[tex]\qquad \qquad \mathbb{R}^{\mathbb{R}}=\{f: \, \mathbb{R}\rightarrow \mathbb{R}, \, [/tex] funções [tex]\}[/tex].
✐ A soma de [tex]f[/tex] e [tex]g[/tex] é a função denotada por [tex]f+g[/tex] e assim definida:
[tex]\qquad \begin{align*} f+g: \, & \mathbb{R} \rightarrow \mathbb{R}\\ & \left( f+g \right)(x)=f(x)+g(x) \end{align*}[/tex]
✐ O produto de [tex]f[/tex] e [tex]g[/tex] é a função denotada por [tex]f\cdot g[/tex] e assim definida:
[tex]\qquad\begin{align*} f\cdot g: \, & \mathbb{R} \rightarrow \mathbb{R}\\ & \left( f\cdot g \right)(x)=f(x)\cdot g(x) \end{align*}[/tex]
✐ A composta de [tex]f[/tex] e [tex]g[/tex] é a função denotada por [tex]f\circ g[/tex] e assim definida:
[tex]\qquad\begin{align*} f\circ g: \, & \mathbb{R} \rightarrow \mathbb{R}\\ & \left(f\circ g\right) \left(x\right)=f\left(g\left(x\right)\right) \end{align*}[/tex]
A partir da definição da soma, do produto e da composta de duas funções de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex], podemos definir três operações binárias no conjunto [tex]\mathbb{R}^{\mathbb{R}}[/tex] e com isso definir uma estrutura matemática para esse conjunto. (Você se lembra do que é uma operação?)
|
✐ A operação adição em [tex]\mathbb{R}^{\mathbb{R}}[/tex] é a função de [tex]\mathbb{R}^{\mathbb{R}}\times \mathbb{R}^{\mathbb{R}}[/tex] em [tex]\mathbb{R}^{\mathbb{R}}[/tex] que a cada par ordenado de funções [tex](f,g)[/tex] associa a função soma [tex]f+g[/tex] acima definida: [tex]\begin{align*} +: \mathbb{R}^{\mathbb{R}} \times \mathbb{R}^{\mathbb{R}} &\rightarrow \mathbb{R}^{\mathbb{R}} \\ (f,g) &\mapsto f+g \end{align*}[/tex]
✐ A operação multiplicação em [tex]\mathbb{R}^{\mathbb{R}}[/tex] é a função de [tex]\mathbb{R}^{\mathbb{R}}\times \mathbb{R}^{\mathbb{R}}[/tex] em [tex]\mathbb{R}^{\mathbb{R}}[/tex] que a cada par ordenado de funções [tex](f,g)[/tex] associa a função produto [tex]f\cdot g[/tex] acima definida:
✐ A operação composição em [tex]\mathbb{R}^{\mathbb{R}}[/tex] é a função de [tex]\mathbb{R}^{\mathbb{R}}\times \mathbb{R}^{\mathbb{R}}[/tex] em [tex]\mathbb{R}^{\mathbb{R}}[/tex] que a cada par ordenado de funções [tex](f,g)[/tex] associa a função composta [tex]f\circ g[/tex] acima definida:
Essas três operações são ditas operações internas ou operações fechadas em [tex]\mathbb{R}^{\mathbb{R}}[/tex]. |
 |
Para nossa discussão, precisaremos definir duas funções específicas que vão desempenhar um papel importante na estrutura que iremos definir para o conjunto [tex]\mathbb{R}^{\mathbb{R}}[/tex] (algo como o papel que o zero e o um exercem nos conjuntos numéricos, com relação à adição e à multiplicação, respectivamente).
✐ Chamamos de função nula a função [tex]0_{\mathbb{R}}: \mathbb{R} \rightarrow \mathbb{R}[/tex] dada por [tex]0_{\mathbb{R}}(x)=0[/tex], ou seja a função que associa a qualquer número real o número [tex]0[/tex].
✐ Chamamos de função um a função [tex]1_{\mathbb{R}}: \mathbb{R} \rightarrow \mathbb{R}[/tex] dada por [tex]1_{\mathbb{R}}(x)=1[/tex], isto é a função que associa a qualquer número real o número [tex]1[/tex].
Essas duas funções são ditas funções constantes, pois sempre associam respectivamente uma mesma imagem a todos os números reais. Dessa forma elas são funções não injetoras. Observem que também são funções não sobrejetoras, uma vez que [tex]Im(0_{\mathbb{R}})=\{0\}\ne \mathbb{R}[/tex] e [tex]Im(1_{\mathbb{R}})=\{1\}\ne \mathbb{R}[/tex].
Para efeito do que está por vir, vamos também precisar de duas funções associadas a uma dada função [tex]f[/tex]: a função [tex]-f[/tex] e a função [tex]\dfrac{1}{f}[/tex].
✐ Chamamos oposta de [tex]f[/tex] a função denotada por [tex]-f[/tex] e assim definida:
[tex]\qquad \qquad \begin{align*} -f: \, & \mathbb{R} \rightarrow \mathbb{R}\\ & \left( -f \right)(x)=-f(x). \end{align*}[/tex]
✐ Chamamos de função [tex]\dfrac{1}{f}[/tex] a função assim definida:
[tex]\qquad \qquad \begin{align*} \dfrac{1}{f}: \, & \mathbb{R} \rightarrow \mathbb{R}\\ & \left( \dfrac{1}{f} \right)(x)=\dfrac{1}{f(x)}, f(x)\ne 0. \end{align*}[/tex]
Cuidado para não confundir notações: [tex]\dfrac{1}{f} \ne f^{-1}[/tex].
Observem também que as condições de definição são diferentes: a função [tex]\dfrac{1}{f}[/tex] está definida para qualquer número real [tex]x[/tex] tal que [tex]f(x)\ne 0[/tex] e para que [tex] f^{-1}[/tex] esteja definida [tex]f[/tex] deve ser bijetora.
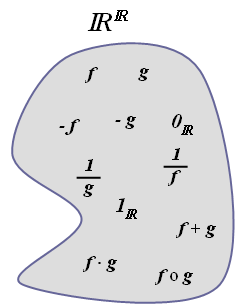
Com essas últimas definições, ficamos com uma nova visão matemática do conjunto [tex]\mathbb{R}^{\mathbb{R}}[/tex], uma vez que, se [tex]f, \, g[/tex] são elementos genéricos do conjunto [tex]\mathbb{R}^{\mathbb{R}}[/tex], também são elementos de [tex]\mathbb{R}^{\mathbb{R}}[/tex]:
- [tex]f+g; \, \, f\cdot g; \, \, -f; \, \, -g; \, \, f\circ g; [/tex] [tex]\dfrac{1}{g}[/tex], para valores reais [tex]x[/tex] tais que [tex]g(x)\ne 0[/tex]; [tex]\dfrac{1}{f}[/tex], para valores reais [tex]x[/tex] tais que [tex]f(x)\ne 0[/tex]; além das funções [tex]0_{\mathbb{R}}; \, \, 1_{\mathbb{R}}[/tex].
Não mencionaremos neste momento as inversas [tex] f^{-1}[/tex] e [tex] g^{-1}[/tex], pois elas dependem de qualidades intrínsecas das funções [tex]f[/tex] e [tex]g[/tex] e não do conjunto [tex] \mathbb{R}^{\mathbb{R}}[/tex].
Esse olhar matemático é importante para se definir, por exemplo, uma estrutura algébrica para o conjunto [tex]\mathbb{R}^{\mathbb{R}}[/tex]. Isso mesmo, uma estrutura algébrica…
Vamos fazer aqui um (não pequeno) parêntesis.
 |
Com maior ou menor rigor, trechos desta conversinha são comuns em cursos universitários na área de Computação e Informática e em uma disciplina chamada Álgebra Linear, comum aos cursos de Engenharia, Matemática e Física. |
Suponha, por exemplo, que em um conjunto [tex]A[/tex] não vazio definamos uma operação binária:
[tex]\qquad \qquad *: A\times A \rightarrow A[/tex] (Uma operação é uma função, não é mesmo?).
Intuitivamente, isso significa que podemos operar com elementos quaisquer de [tex]A[/tex] e, a partir de cada par deles, definir um terceiro elemento. Indicaremos essa estrutura por [tex](A,*)[/tex].
Para as estruturas algébricas, particularmente interessam as seguintes propriedades :
- Comutatividade
- Associatividade
- Existência de elemento neutro
- Existência de elementos simetrizáveis
O que seriam essas propriedades? Vamos lá.
✐ A operação [tex]*[/tex] é dita comutativa em [tex]A[/tex] se a seguinte condição for satisfeita:
[tex]\qquad \qquad a * b = b * a, \, \forall a,b ∈ A[/tex]
✐ A operação [tex]*[/tex] é dita associativa em [tex]A[/tex] se a seguinte condição for satisfeita:
[tex]\qquad \qquad a * (b * c) = (a * b) * c, \, \forall a,b,c ∈ A[/tex]
✐ A operação [tex]*[/tex] tem elemento neutro em [tex]A[/tex] se a seguinte condição for satisfeita:
[tex]\qquad \qquad \exists \, \text{e} ∈ A[/tex] tal que [tex] a * \text{e} = \text{e} * a = a, \forall a ∈ A[/tex]
✐ Um elemento [tex]a \in A[/tex] é dito simetrizável com relação a operação [tex]*[/tex] se a seguinte condição for satisfeita:
[tex]\qquad \qquad \exists \, a’ ∈ A[/tex] tal que [tex]a * a’ = a’ * a = \text{e}[/tex]
Para cada [tex] a ∈ A[/tex], o elemento [tex] a’ ∈ A[/tex] tal que [tex] a * a’ = a’ * a = \text{e}[/tex] é dito o simétrico de [tex] a[/tex]. Dependendo da operação utilizada, o simétrico de um elemento recebe nomes especiais como oposto ou inverso.
Acharam pesada a escrita?
Pois saibam que aliviamos as notações; cliquem no botão abaixo e vejam como essas propriedades são comumente definidas em uma aula de Matemática Discreta e Álgebra de cursos de Computação.
✐ A tabela abaixo mostra como uma estrutura [tex](A,*)[/tex] pode ser classificada, de acordo com as propriedades que a estrutura tem.
| Nome da Estrutura | Associatividade | Comutatividade | Elemento neutro | Elementos simetrizáveis |
| Grupoide | ||||
| Semigrupo | ✓ | |||
| Semigrupo abeliano | ✓ | ✓ | ||
| Monoide | ✓ | ✓ | ||
| Monoide abeliano | ✓ | ✓ | ✓ | |
| Grupo | ✓ | ✓ | Todos os elementos de [tex]A[/tex] são simetrizáveis. | |
| Grupo abeliano | ✓ | ✓ | ✓ | Todos os elementos de [tex]A[/tex]são simetrizáveis. |
Assim, por exemplo, [tex](\mathbb{N},+)[/tex] é um monoide abeliano; [tex](\mathbb{Z},+)[/tex] é um grupo abeliano; [tex](\mathbb{Z},\times)[/tex] é um monoide abeliano. Se considerarmos o conjunto [tex]\mathbb{Z}_p[/tex], estudado no PIC, munido da adição modular, [tex](\mathbb{Z}_p,+)[/tex] é um grupo abeliano. Também, [tex](\mathbb{Q^*},\cdot)[/tex] é um grupo abeliano e [tex](\mathbb{R^*},\cdot)[/tex] é um grupo abeliano ([tex]\mathbb{Q^*}, \, \mathbb{R^*}[/tex]: respectivamente, conjunto dos racionais não nulos e dos reais não nulos).
✐ Uma estrutura com duas operações internas [tex](A,*, \diamond)[/tex] pode ser também classificada de acordo com as propriedades que ela tem. Neste caso, é interessante apresentarmos uma propriedade que relaciona as duas operações: a distributividade da operação [tex]\diamond[/tex], com relação à operação [tex]*[/tex].
✐ Dizemos que a operação [tex]\diamond[/tex] é distributiva com relação à operação [tex]*[/tex] se as seguintes condições forem satisfeitas:
[tex]\qquad \qquad a\diamond(b*c)=a\diamond b*a\diamond c \, \, [/tex] e [tex] \, \, (b*c)\diamond a=b\diamond a*c\diamond a, \, \forall a,b,c\in A[/tex]
Por exemplo, suponha que em conjunto [tex]A[/tex] possamos definir uma adição e uma multiplicação.
Se [tex](A,+)[/tex] for um grupo abeliano, [tex] \times[/tex] for associativa em [tex] A[/tex] e a operação multiplicação for distributiva com relação a operação adição ([tex]a\times(b+c)=a\times b+a\times c[/tex] e [tex](b+c)\times a=b\times a+c\times a, \, \forall a,b,c\in A[/tex]), então a estrutura [tex](A,+, \times )[/tex] é chamada de anel. Um anel no qual a multiplicação seja comutativa é dito um anel abeliano ou comutativo.
Pelo exposto, os conjuntos [tex]\mathbb{Z}[/tex], [tex]\mathbb{Q}[/tex] e [tex]\mathbb{R}[/tex] munidos de suas respectivas adições e multiplicações são todos anéis comutativos; na verdade, como eles têm elementos neutros multiplicativos, eles são ditos anéis comutativos com unidade. Aprofundando mais, como também todos os elementos não nulos de [tex]\mathbb{Q}[/tex] e de [tex]\mathbb{R}[/tex] têm simétricos multiplicativos (inversos), as estruturas [tex](\mathbb{Q},+, \times)[/tex] e [tex](\mathbb{R},+, \times)[/tex] são exemplos do que chamamos na Matemática de corpos.
A estrutura algébrica que é estudada a fundo na Álgebra Linear é um pouco diferente das que apresentamos: ela envolve um conjunto não vazio [tex]V[/tex], um corpo numérico [tex]K[/tex] ([tex]K=\mathbb{R}[/tex] ou [tex]K=\mathbb{C}[/tex]) e duas operações: uma adição interna em [tex]V[/tex] e uma multiplicação externa, chamada de “multiplicação por escalar” (ambas são funções):
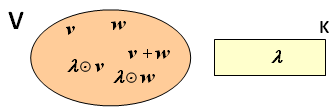
[tex]\qquad \qquad \begin{align*} +: V \times V &\rightarrow V \\ (a,b) &\mapsto a+b \end{align*}\qquad [/tex] e [tex]\qquad \begin{align*} \odot: K \times V &\rightarrow V \\ (\gamma,a) &\mapsto \gamma\odot a \end{align*}[/tex]
O nome dessa estrutura é “Espaço Vetorial”, mas não vamos tratar dela por aqui, para não prolongar ainda mais esta pequena introdução às estruturas algébricas.
No entanto, vocês podem observar na figura acima os efeitos distintos das duas operações, a interna [tex]+[/tex] e a externa [tex]\odot [/tex], e o fato de se operar com objetos matemáticos distintos: um do conjunto [tex]V[/tex] e outro do conjunto [tex]K[/tex].
Dito isso, que estrutura podemos definir para o conjunto [tex]\mathbb{R}^{\mathbb{R}}[/tex]?
Vamos considerar o conjunto [tex]\mathbb{R}^{\mathbb{R}}[/tex] munido das operações internas:
[tex]\qquad \begin{align*} +: \mathbb{R}^{\mathbb{R}} \times \mathbb{R}^{\mathbb{R}} &\rightarrow \mathbb{R}^{\mathbb{R}} \\ (f,g) &\mapsto f + g \end{align*}\qquad [/tex] [tex]\qquad \begin{align*} \cdot: \mathbb{R}^{\mathbb{R}} \times \mathbb{R}^{\mathbb{R}} &\rightarrow \mathbb{R}^{\mathbb{R}} \\ (f,g) &\mapsto f\cdot g \end{align*}\qquad[/tex] [tex]\qquad \begin{align*} \circ: \mathbb{R}^{\mathbb{R}} \times \mathbb{R}^{\mathbb{R}} &\rightarrow \mathbb{R}^{\mathbb{R}} \\ (f,g) &\mapsto f\circ g \end{align*}[/tex]
e observar que propriedades essas operações satisfazem, ou não.(Aqui temos uma boa oportunidade para praticarmos a negação de proposições)
| Operação | Associatividade | Comutatividade | Elemento neutro | Elementos simetrizáveis |
| [tex]+[/tex] | [tex](f+g)+h=f+(g+h), \, \forall f,g,h \in \mathbb{R}^{\mathbb{R}}[/tex] | [tex]f+g=g+f, \, \forall f,g \in \mathbb{R}^{\mathbb{R}}[/tex] | [tex]0_{\mathbb{R}}[/tex] | [tex]\forall f \in \mathbb{R}^{\mathbb{R}}, \, \exists (-f)\in \mathbb{R}^{\mathbb{R}} [/tex] |
| [tex]\cdot[/tex] | [tex](f\cdot g)\cdot h=f\cdot(g\cdot h), \, \forall f,g,h \in \mathbb{R}^{\mathbb{R}}[/tex] | [tex]f\cdot g=g\cdot f, \, \forall f,g \in \mathbb{R}^{\mathbb{R}}[/tex] | [tex]1_{\mathbb{R}}[/tex] | [tex]\exists f \in \mathbb{R}^{\mathbb{R}}; \, \not\exists \dfrac{1}{f}\in \mathbb{R}^{\mathbb{R}} [/tex] |
| [tex]\circ[/tex] | [tex](f\circ g)\circ h=f\circ (g\circ h), \, \forall f,g,h \in \mathbb{R}^{\mathbb{R}}[/tex] | [tex]\exists f,g \in \mathbb{R}^{\mathbb{R}};f\circ g\ne g\circ f[/tex] | [tex]id_{\mathbb{R}^{\mathbb{R}}}[/tex] | [tex]\exists f \in \mathbb{R}^{\mathbb{R}}; \, \not\exists f^{-1}\in \mathbb{R}^{\mathbb{R}} [/tex] |
Assim:
- [tex]\left(\mathbb{R}^{\mathbb{R}},+\right)[/tex] é um grupo comutativo.
- [tex]\left(\mathbb{R}^{\mathbb{R}},\cdot \right)[/tex] é um monoide abeliano.
- [tex]\left(\mathbb{R}^{\mathbb{R}}, \circ\right)[/tex] é um monoide.
Como sabemos que
[tex]\qquad \qquad f\circ (g+h)=f\circ g+f\circ h[/tex] e [tex](g+h)\circ f=g\circ f+h\circ f, \, \forall a,b,c\in A[/tex],
então
- [tex]\left(\mathbb{R}^{\mathbb{R}},+ , \cdot\right)[/tex] é um anel comutativo com unidade.
Vamos tentar melhorar essa classificação das funções de [tex]\mathbb{R}[/tex] em [tex]\mathbb{R}[/tex]. Para tanto, fixado um conjunto não vazio [tex]E[/tex], vamos denotar por [tex]S(E)[/tex] o conjunto das bijeções de [tex]E[/tex] em [tex]E[/tex]:
[tex]\qquad \qquad S(E)=\{f: \, E \rightarrow E, \, [/tex] bijeções[tex]\}[/tex].
Assim definido, [tex]S(E)[/tex] é denominado o “conjunto das permutações de [tex]E[/tex]”. Os estudos de vocês sobre funções nos garantem que a composição é uma operação interna para [tex]S(E)[/tex]:
[tex]\qquad \begin{align*} \circ: S(E) \times S(E) &\rightarrow S(E) \\ (f,g) &\mapsto f \circ g \end{align*}\qquad [/tex]
e também nos permitem montar a seguinte tabela com as propriedades da composição de funções em [tex]S(E)[/tex]:
| Operação | Associatividade | Comutatividade | Elemento neutro | Elementos simetrizáveis |
| [tex]\circ[/tex] | [tex](f\circ g)\circ h=f\circ (g\circ h)[/tex] | Não tem a propriedade | [tex]id_{S(E)}[/tex] | [tex]f^{-1} [/tex] |
Portanto, a estrutura [tex]\left(S(E),\circ \right)[/tex] é um grupo não abeliano e, considerando particularmente [tex]E=\mathbb{R}[/tex], podemos ampliar a conclusão sobre o conjunto [tex]\mathbb{R}^{\mathbb{R}}[/tex] obtida acima:
- [tex]\left(\mathbb{R}^{\mathbb{R}},+\right)[/tex] é um grupo comutativo.
- [tex]\left(\mathbb{R}^{\mathbb{R}},\cdot \right)[/tex] é um monoide abeliano.
- [tex]\left(\mathbb{R}^{\mathbb{R}},+ , \cdot\right)[/tex] é um anel comutativo com unidade.
- [tex]\left(\mathbb{R}^{\mathbb{R}}, \circ\right)[/tex] é um monoide.
- [tex]\left(S(\mathbb{R}),\circ \right)[/tex] é um grupo.
Alguém pode estar se perguntando para que servem as estruturas?
Estruturas genéricas são uma maneira “econômica” de se estudar conjuntos que tenham o mesmo comportamento com relação a determinadas operações.
Por exemplo, se [tex](A,*)[/tex] é um grupo, sabemos que todo elemento de [tex]A[/tex] tem um simétrico; mas, quantos simétricos tem cada elemento de [tex]A[/tex]?
Esta é uma pergunta rápida de se responder: todos elementos de um grupo têm um único simétrico. E a demonstração é simples, veja:
Suponha que [tex]a \in A[/tex] e que existam elementos [tex]a’, a” \in A[/tex] tais que [tex]\boxed{a * a’ = a’ * a = \text{e}} \, [/tex] e [tex] \, \boxed{a * a” = a” * a = \text{e}}[/tex]. Logo,
[tex]\qquad \qquad a’=a’* \text{e}=a’*(a * a” )=(a’*a)*a”=\text{e}*a”=a”[/tex],
ou seja, [tex] a’=a”[/tex] e o simétrico de qualquer elemento [tex]a\in A[/tex] é único.
Mais importante do que entender a demonstração é vocês perceberem que a propriedade mostrada vale para todos os conjuntos que definem uma estrutura de grupo com relação a alguma operação, seja ele qual for. Entre outros, podemos, então, afirmar que:
- cada número inteiro tem um único oposto;
- cada número racional tem um único oposto;
- cada número real tem um único oposto;
- cada número racional não nulo tem um único inverso;
- cada número real não nulo tem um único inverso;
- cada função de [tex] \mathbb{R}[/tex] em [tex] \mathbb{R}[/tex] tem uma única oposta;
- toda bijeção tem uma única inversa;
ou seja, provamos que todo elemento de um conjunto que, com relação a uma determinada operação, seja um grupo tem um único simétrico.
Que economia de raciocínio, hem?
Dessa forma, ao estudarmos genericamente as propriedades de um grupo, estaremos estudando particularmente as propriedades de qualquer estrutura [tex](A,*)[/tex] que seja um grupo. Ao estudarmos genericamente as propriedades de um anel, estaremos estudando particularmente as propriedades de qualquer estrutura [tex](A,*,\diamond)[/tex] que seja um anel, e assim por diante…
Dentro dessa característica das estruturas algébricas, existe um resultado que facilita ainda mais trabalhar simultaneamente com vários grupos, por mais abstratos que sejamos seus elementos: o Teorema de Cayley. Informalmente, esse teorema garante que, para estudarmos genericamente um grupo [tex]\left(A,*\right)[/tex], basta estudarmos um grupo de permutações conveniente.
Com a apresentação, mesmo que informal, do Teorema de Cayley, não poderíamos deixar de mencionar um caso particular e muitíssimo importante de grupos de permutações: aquele em que [tex]E[/tex] é um conjunto finito. Se [tex]E= \{1,2, …, n\}[/tex] e [tex]n \ge 1[/tex], a notação [tex]S(E)[/tex] é simplificada para [tex]S_n[/tex] e o grupo [tex]\left(S_n,\circ \right)[/tex] recebe o nome especial de grupo simétrico de grau [tex]n[/tex] e é dito um grupo finito, pelo fato de [tex]E[/tex] ter um número finito de elementos. Neste caso, cada função que compõe o conjunto [tex]S_n[/tex] pode ser interpretada como uma permutação dos elementos do conjunto [tex]\{1, 2, …, n\}[/tex] e tem também uma notação especial:
- se [tex]f \in S_n[/tex], utilizamos as imagens [tex]f(1),f(2),\cdots,f(n)[/tex] e escrevemos [tex]f[/tex] na forma
[tex]\qquad \qquad f=\left(\begin{array}{c c c c c}
1&\cdots&i&\cdots&n\\
\, f(1)&\cdots&f(i)&\cdots&f(n)
\end{array}
\right)[/tex].
Com essa notação as permutações [tex]\left(3,4,1,2,5\right)[/tex], [tex]\left(1, 2, 5, 4, 3\right)[/tex] e [tex]\left(5,4,3,2,1\right)[/tex] dos elementos [tex]\left(1,2,3,4,5\right)[/tex], por exemplo, se indicadas por:
[tex]\left(
\begin{array}{c c c c c}
1&2&3&4&5\\
3&4&1&2&5
\end{array}
\right)
\, \,
\left(
\begin{array}{c c c c c}
1&2&3&4&5\\
1&2&5&4&3
\end{array}
\right)
\, \, \, \, \left(
\begin{array}{c c c c c}
1&2&3&4&5\\
5&4&3&2&1
\end{array}
\right)
\, \, \, \,
[/tex]
podem ser consideradas elementos do conjunto [tex]S_5[/tex].
Todas as permutações de [tex]\left(1, 2, 3\right)[/tex] podem ser consideradas funções e indicadas por
[tex]
f_1=\left(
\begin{array}{c c c }
1&2&3\\
1&2&3
\end{array}
\right)
\, \,
f_2=\left(
\begin{array}{c c c }
1&2&3\\
1&3&2
\end{array}
\right)
\, \,
f_3=\left(
\begin{array}{c c c }
1&2&3\\
2&1&3
\end{array}
\right)
\, \,
f_4=\left(
\begin{array}{c c c }
1&2&3\\
2&3&1
\end{array}
\right)
\, \,
f_5=\left(
\begin{array}{c c c }
1&2&3\\
3&1&2
\end{array}
\right)
\, \,
f_6=\left(
\begin{array}{c c c }
1&2&3\\
3&2&1
\end{array}
\right)
[/tex]
e, assim, [tex]S_5=\{f_1,f_2,f_3,f_4,f_5,f_6 \}[/tex].
Uma argumentação muito simples e que utiliza a análise combinatória que vocês aprenderam em várias edições do PIC pode mostrar que [tex]S_n[/tex] tem [tex]n![/tex] elementos. Em particular, todo grupo [tex](A,*)[/tex] com [tex]n![/tex] elementos pode ser estudado via o grupo [tex](S_n,\circ)[/tex]
Poxa, quem diria que aquelas permutações que vocês aprenderam em análise combinatória seriam funções?
E, ainda, funções que permitem estudar grupos finitos quaisquer!
 |
Até uma próxima oportunidade, pessoal! |
Equipe COM – OBMEP
