Regra de Chió
Considere uma matriz [tex]M[/tex] de ordem [tex]n\geq 2[/tex], tal que [tex]a_{11}=1[/tex], ou seja,
[tex]\qquad M = \begin{bmatrix}
1 & a_{12} & a_{13} & a_{14}& \cdots & a_{1n}\\
a_{21} & a_{22} & a_{23} & a_{24}& \cdots & a_{2n}\\
a_{31} & a_{32} & a_{33} & a_{34}& \cdots & a_{3n}\\
a_{41} & a_{42} & a_{43} & a_{44}& \cdots & a_{4n}\\
\vdots & \vdots & \vdots & \vdots& \ddots & \vdots\\
a_{n1} & a_{n2} & a_{n3} & a_{n4}& \cdots & a_{nn}
\end{bmatrix}.[/tex]
A partir da matriz [tex]M[/tex] vamos formar uma matriz [tex]M'[/tex], seguindo os próximos n-1 passos:
[tex]\qquad[/tex] 1) adicionamos à segunda coluna o resultado da multiplicação de [tex]-a_{12}[/tex] pela primeira coluna;
[tex]\qquad[/tex] 2) adicionamos à terceira coluna o resultado da multiplicação de [tex]-a_{13}[/tex] pela primeira coluna;
[tex]\qquad[/tex] 3) adicionamos à quarta coluna o resultado da multiplicação de [tex]-a_{14}[/tex] pela primeira coluna;
e assim por diante, até
[tex]\qquad[/tex] n-1) adicionarmos à n-ésima coluna o resultado da multiplicação de [tex]-a_{1n}[/tex] pela primeira coluna.
Assim, teremos a matriz [tex]M'[/tex], dada por
[tex]\qquad M’ = \begin{bmatrix}
1 & a_{12}-a_{12} & a_{13}-a_{13} & a_{14}-a_{14}& \cdots & a_{1n}-a_{1n}\\
a_{21} & a_{22}-a_{21}a_{12} & a_{23}-a_{21}a_{13} & a_{24}-a_{21}a_{14}& \cdots & a_{2n}-a_{21}a_{1n}\\
a_{31} & a_{32}-a_{31}a_{12} & a_{33}-a_{31}a_{13} & a_{34}-a_{31}a_{14}& \cdots & a_{3n}-a_{31}a_{1n}\\
a_{41} & a_{42}-a_{41}a_{12} & a_{43}-a_{41}a_{13} & a_{44}-a_{41}a_{14}& \cdots & a_{4n}-a_{41}a_{1n}\\
\vdots & \vdots & \vdots & \vdots& \ddots & \vdots\\
a_{n1} & a_{n2}-a_{n1}a_{12} & a_{n3}-a_{n1}a_{13} & a_{n4}-a_{n1}a_{14}& \cdots & a_{nn}-a_{n1}a_{1n}
\end{bmatrix},[/tex]
ou seja,
[tex]\qquad M’ = \begin{bmatrix}
1 & 0 & 0& 0& \cdots & 0\\
a_{21} & a_{22}-a_{21}a_{12} & a_{23}-a_{21}a_{13} & a_{24}-a_{21}a_{14}& \cdots & a_{2n}-a_{21}a_{1n}\\
a_{31} & a_{32}-a_{31}a_{12} & a_{33}-a_{31}a_{13} & a_{34}-a_{31}a_{14}& \cdots & a_{3n}-a_{31}a_{1n}\\
a_{41} & a_{42}-a_{41}a_{12} & a_{43}-a_{41}a_{13} & a_{44}-a_{41}a_{14}& \cdots & a_{4n}-a_{41}a_{1n}\\
\vdots & \vdots & \vdots & \vdots& \ddots & \vdots\\
a_{n1} & a_{n2}-a_{n1}a_{12} & a_{n3}-a_{n1}a_{13} & a_{n4}-a_{n1}a_{14}& \cdots & a_{nn}-a_{n1}a_{1n}
\end{bmatrix}.[/tex]
Pelo teorema de Jacobi, temos [tex]\det M= \det M'[/tex].
Por outro lado, aplicando o teorema de Laplace na primeira linha da matriz [tex]M'[/tex], temos
[tex]\qquad \det M’ = 1\cdot C_{11}+0\cdot C_{12}+0\cdot C_{13}+0\cdot C_{14}+\cdots +0\cdot C_{1n}[/tex]
[tex]\qquad \det M’ = 1\cdot C_{11}[/tex]
[tex]\qquad \det M’ = 1\cdot (-1)^{1+1}D_{11}[/tex]
[tex]\qquad \det M’ = D_{11}[/tex],
onde
[tex]\qquad D_{11} = \begin{vmatrix}
a_{22}-a_{21}a_{12} & a_{23}-a_{21}a_{13} & a_{24}-a_{21}a_{14}& \cdots & a_{2n}-a_{21}a_{1n}\\
a_{32}-a_{31}a_{12} & a_{33}-a_{31}a_{13} & a_{34}-a_{31}a_{14}& \cdots & a_{3n}-a_{31}a_{1n}\\
a_{42}-a_{41}a_{12} & a_{43}-a_{41}a_{13} & a_{44}-a_{41}a_{14}& \cdots & a_{4n}-a_{41}a_{1n}\\
\vdots & \vdots & \vdots& \ddots & \vdots\\
a_{n2}-a_{n1}a_{12} & a_{n3}-a_{n1}a_{13} & a_{n4}-a_{n1}a_{14}& \cdots & a_{nn}-a_{n1}a_{1n}
\end{vmatrix}.[/tex]
Portanto, temos
[tex]\qquad \det M = \det M’ = D_{11}[/tex]
[tex]\qquad \det M = \begin{vmatrix}
a_{22}-a_{21}a_{12} & a_{23}-a_{21}a_{13} & a_{24}-a_{21}a_{14}& \cdots & a_{2n}-a_{21}a_{1n}\\
a_{32}-a_{31}a_{12} & a_{33}-a_{31}a_{13} & a_{34}-a_{31}a_{14}& \cdots & a_{3n}-a_{31}a_{1n}\\
a_{42}-a_{41}a_{12} & a_{43}-a_{41}a_{13} & a_{44}-a_{41}a_{14}& \cdots & a_{4n}-a_{41}a_{1n}\\
\vdots & \vdots & \vdots& \ddots & \vdots\\
a_{n2}-a_{n1}a_{12} & a_{n3}-a_{n1}a_{13} & a_{n4}-a_{n1}a_{14}& \cdots & a_{nn}-a_{n1}a_{1n}
\end{vmatrix}.[/tex]
Observe que reduzimos o problema de calcular o determinante de uma matriz de ordem [tex]n[/tex], ao cálculo do determinante de uma matriz de ordem [tex]n−1[/tex] (uma vez que a última matriz representada acima é de ordem [tex]n-1[/tex]), tornando o processo mais simples. A este processo atribuímos o nome de Regra de Chió.
Exemplo: Utilize a regra de Chió e calcule o determinante da matriz
[tex]\qquad M=\begin{bmatrix}
1 & 3 & 1 & 4 \\
-1 & 0 & 2 & -2 \\
3 & 1 & -1 & 0 \\
0 & 4 & -2 & 3 \\
\end{bmatrix}.[/tex]
Solução: Vamos encontrar, de forma mais direta, a matriz [tex]M'[/tex] obtida segundo os passos da regra de Chió:
[tex]\qquad M’=\begin{bmatrix}
1&0&0&0\\
-1&0-(-1)\cdot 3 & 2-(-1)\cdot 1 & -2 -(-1)\cdot 4\\
3&1-3\cdot 3 & -1-3\cdot 1 & 0-3\cdot 4 \\
0&4-0\cdot 3 & -2-0\cdot 1 & 3-0\cdot 4 \\
\end{bmatrix}[/tex]
[tex]\qquad M’=\begin{bmatrix}
1&0&0&0\\
-1&3 & 3 & 2\\
3&-8& -4& -12\\
0&4& -2& 3\\
\end{bmatrix}.[/tex]
Portanto,
[tex]\qquad \det M = \det M’ = \begin{vmatrix}
3 & 3 & 2\\
-8& -4& -12\\
4& -2& 3\\
\end{vmatrix} = -116[/tex].
 |
Neste momento, você deve estar se perguntando: “E se o elemento [tex]a_{11}[/tex] for diferente de [tex]1[/tex], então tudo isso é em vão?”. Calma! Ainda assim, você poderá usar a Regra de Chió. Atente para as observações abaixo. |
Observações:
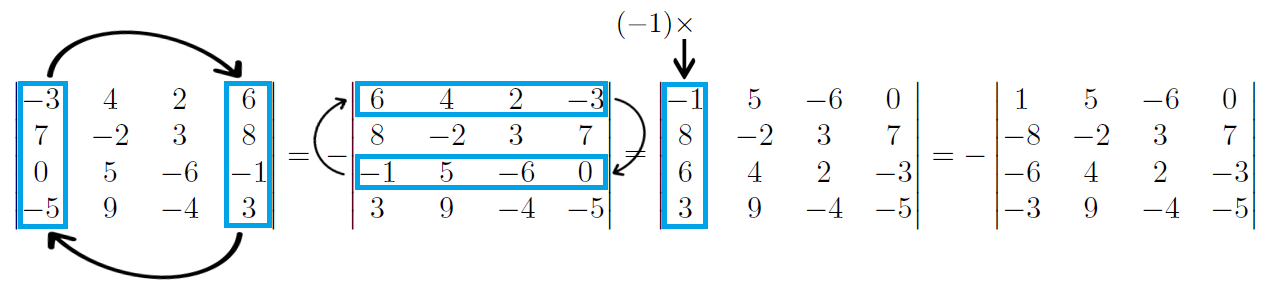
[tex]\qquad [/tex]1) Se tivermos, na matriz [tex]M[/tex], [tex]a_{11}\neq 1[/tex], e existir algum outro elemento igual a [tex]1[/tex] (ou [tex]-1[/tex]) na matriz, então podemos, através da propriedade de troca de filas paralelas, transformar [tex]M[/tex] em uma matriz [tex]M'[/tex] que tenha [tex]a_{11}=1[/tex]. Veja exemplos de situações possíveis:
- quando existe algum elemento igual a [tex]1[/tex], na matriz:
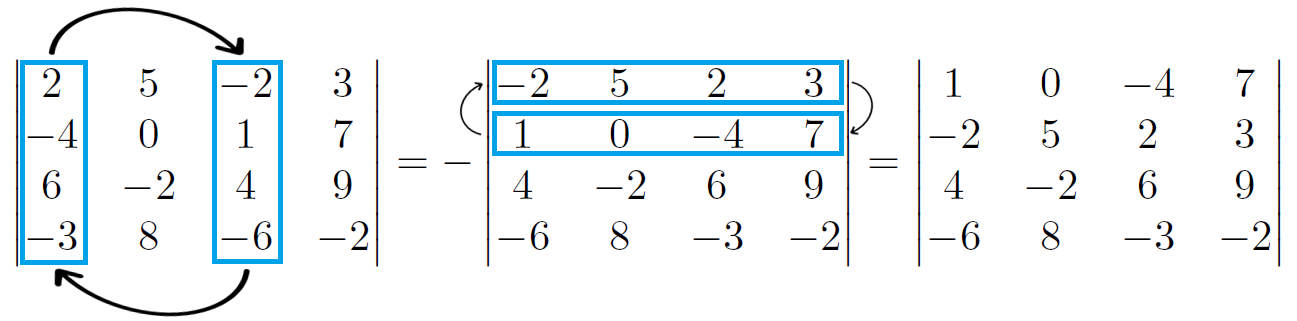
- quando não existe elemento igual a [tex]1[/tex], mas existe algum elemento igual a [tex]-1[/tex], na matriz:
[tex]\qquad [/tex]2) Se não tivermos, na matriz [tex]M[/tex], nenhum elemento igual a [tex]1[/tex] ou [tex]-1[/tex], então podemos, através do teorema de Jacobi, transformar [tex]M[/tex] em uma matriz [tex]M'[/tex] que tenha [tex]a_{11}=1[/tex]. Veja um exemplo:
- Na matriz abaixo, podemos somar à primeira coluna o resultado da segunda multiplicada por [tex]2[/tex], obtendo assim, [tex]a_{11} = 1[/tex]:
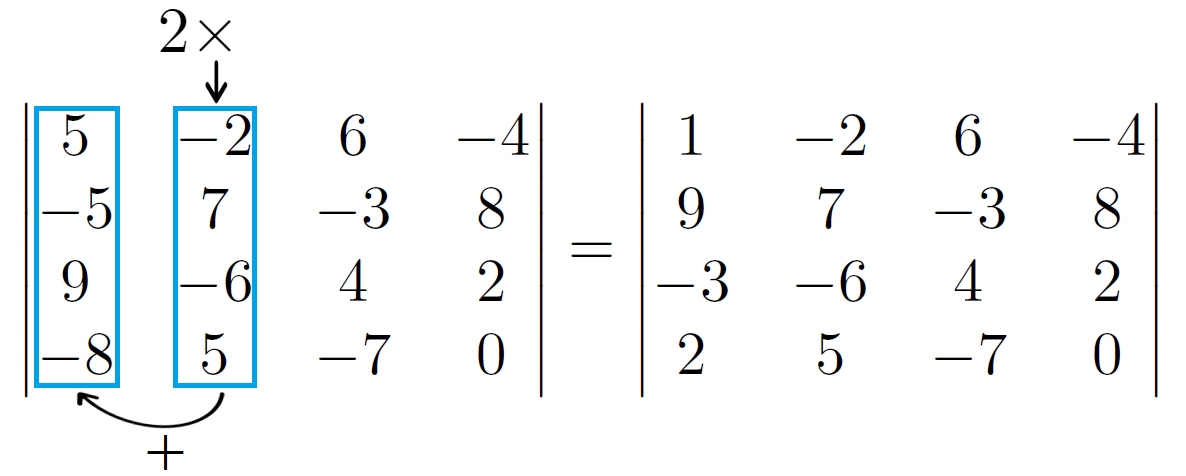
Adentramos agora no estudo das matrizes de Vandermonde, cujo nome é uma homenagem ao ilustre matemático francês Alexandre-Théophile Vandermonde (1735 – 1796).
Matriz de Vandermonde
Chamamos de matriz de Vandermonde toda matriz [tex]M[/tex] de ordem [tex]n\geq 2[/tex], tal que os elementos das colunas de [tex]M[/tex] são formadas por potências de mesma base, com expoente inteiro, variando de [tex]0[/tex] a [tex]n-1[/tex], ou seja, [tex]M[/tex] é matriz de Vandermonde se tiver o seguinte formato:
[tex]\qquad M = \begin{bmatrix}
1 & 1 & 1& \cdots & 1\\
a_1 & a_2 & a_3& \cdots & a_n\\
a_1^2 & a_2^2 & a_3^2& \cdots & a_n^2\\
\vdots & \vdots & \vdots& \ddots & \vdots\\
a_1^{n-1} & a_2^{n-1} & a_3^{n-1}& \cdots & a_n^{n-1}
\end{bmatrix}.[/tex]
Repare que os elementos da j-ésima coluna formam uma progressão geométrica cujo primeiro elemento é [tex]1[/tex] e a razão é [tex]a_j[/tex].
Os elementos da segunda linha ([tex]a_1,a_2,a_3,\cdots,a_n[/tex]) são chamados de elementos característicos da matriz.
Observação: A matriz de Vandermonde também pode aparecer como sendo a transposta da matriz [tex]M[/tex] acima.
Denotamos o determinante da matriz de Vandermonde acima por [tex]V(a_1,a_2,a_3,\cdots,a_n)[/tex]. Dessa forma, como já definimos a regra de formação dos elementos da matriz de Vandermonde, quando colocamos [tex]V(a_1,a_2,a_3,\cdots,a_n)[/tex], fica subentendido de qual matriz estamos querendo calcular o determinante.
Por exemplo, [tex]V(2,3, 4)[/tex] corresponde ao determinante da matriz
[tex]\qquad A=\begin{bmatrix}
1 & 1 & 1\\
2& 3& 4\\
2^2& 3^2 & 4^2\\
\end{bmatrix}.[/tex]
Existe uma expressão para o cálculo do determinante de uma matriz de Vandermonde, sendo ela o produto de todas as diferenças possíveis [tex](a_j-a_i)[/tex], com [tex]i\lt j[/tex], ou seja,
[tex]V(a_1,a_2,a_3,\cdots,a_n) = (a_2-a_1)(a_3-a_1)\cdots (a_n-a_1)(a_3-a_2)(a_4-a_2)\cdots (a_n-a_2)\cdots (a_{n-1}-a_{n-2})(a_n-a_{n-2})(a_n-a_{n-1}).[/tex]
Exemplo: O determinante de Vandermonde da matriz [tex]A[/tex] acima, é
[tex]\qquad V(2,3,4) = (3-2)(4-2)(4-3)[/tex]
[tex]\qquad V(2,3,4) = 2.[/tex]
Exemplo: Determine o determinante da matriz de Vandermonde
[tex]\qquad M= \begin{bmatrix}
1 & 1 & 1 & 1 \\
-2 & 1 & 3 & -4 \\
4 & 1 & 9 & 16 \\
-8 & 1 & 27 & -64 \\
\end{bmatrix}.[/tex]
Solução:
[tex]\qquad V(-2,1,3,-4) = (1-(-2))(3-(-2))(-4-(-2))(3-1)(-4-1)(-4-3)[/tex]
[tex]\qquad V(-2,1,3,-4) = 3\cdot 5\cdot (-2)\cdot 2\cdot (-5)\cdot (-7)[/tex]
[tex]\qquad V(-2,1,3,-4) = -2100.[/tex]
As matrizes de Vandermonde são encontradas com frequência em diversas áreas de aplicação, incluindo finanças, processamento de sinais, rádio cognitivo e comunicações sem fio.
Na Sala de Estudos sobre matrizes, pudemos aprender o conceito de matriz inversa de uma matriz [tex]A[/tex]. O estudo de determinantes é muito importante para determinar a existência ou não de tais matrizes inversas. Vejamos tal aplicação a seguir.
Teorema: Seja [tex]M[/tex] uma matriz quadrada de ordem [tex]n[/tex]. A inversa de [tex]M[/tex] existe se, e somente se, [tex]\det M\neq 0[/tex].
Exemplos: Verifique, em cada caso, se as matrizes possuem inversas.
[tex]\qquad[/tex]a) [tex]A = \begin{bmatrix}
5 & 3 \\
8 & 5 \\
\end{bmatrix}[/tex]
[tex]\qquad[/tex]b) [tex]B = \begin{bmatrix}
1 & 0 & 3 \\
0 & -2 & 0 \\
0 & 0 & 0 \\
\end{bmatrix}[/tex]
Solução:
[tex]\qquad[/tex]a) Note que [tex]\det A = 1\neq 0[/tex]. Portanto, pelo teorema anterior, [tex]A[/tex] admite inversa.
[tex]\qquad[/tex]b) Temos [tex]\det B = 0[/tex]. Portanto, pelo teorema anterior, [tex]B[/tex] não admite inversa.
Equipe COM – OBMEP
