.Problemão: Lançamento da Bola

Problema
(Indicado a partir do 9º ano do E. F.)

Um lateral [tex]L[/tex] faz um lançamento para um atacante [tex]A[/tex], situado [tex]32 [/tex] metros à sua frente em uma linha paralela à lateral do campo de futebol.
A bola, entretanto, segue uma trajetória retilínea, mas não paralela à lateral, e quando passa pela linha de meio-de-campo, está a uma distância de [tex]12 [/tex] metros da linha que une o lateral ao atacante (observe a figura).

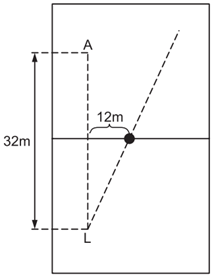
Sabendo-se que a linha de meio-de-campo está à mesma distância dos dois jogadores, qual a distância mínima que o atacante terá de percorrer para encontrar a trajetória da bola?

Solução

A distância mínima que o atacante terá que percorrer para encontrar a trajetória da bola é [tex]MA[/tex], com [tex]M[/tex] um ponto da reta [tex]LC[/tex] tal que [tex]\overline{MA}[/tex] seja perpendicular a [tex]\overline{LM}.[/tex]

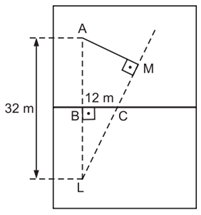
Sejam [tex]B[/tex] e [tex]C[/tex] os pontos onde [tex]\overline{LA}[/tex] e [tex]\overline{LM}[/tex] cruzam a linha do meio de campo, respectivamente.
Como [tex]\overline{LA}[/tex] é paralelo à lateral do campo, [tex]\overline{BC}[/tex] é perpendicular a [tex]\overline{LA}[/tex]. E, uma vez que a linha do meio de campo está à mesma distância dos dois jogadores, [tex]LA=LB=16 \, m.[/tex]
Aplicando o Teorema de Pitágoras ao triângulo [tex]LBC[/tex], temos:
[tex]\qquad \qquad LC^2=LB^2+BC^2 [/tex]
[tex]\qquad \qquad LC=\sqrt{16^2+12^2}=20 \, m.[/tex]
Como [tex]\angle BLC[/tex] e [tex] \angle MLA[/tex] são congruentes, assim como os ângulos [tex]\angle LBC \, [/tex] e [tex] \, \angle LMA[/tex], pelo caso [tex]AA[/tex] temos que os triângulos [tex] BLC \, [/tex] e [tex] \, MLA[/tex] são semelhantes e assim:

[tex]\qquad \qquad \dfrac{LC}{LA}=\dfrac{BC}{MA}[/tex]

[tex]\qquad \qquad \dfrac{20}{32}=\dfrac{12}{MA}[/tex]

[tex]\qquad \qquad \boxed{MA=19,2 \, m} \, .[/tex]

Solução elaborada pelos Moderadores do Blog.