Problema
(Indicado a partir do 9º ano do E. F.)
Uma pista retangular para caminhada mede [tex]100 \, m[/tex] por [tex]250 \, m[/tex]. Deseja-se marcar um ponto [tex]P[/tex], conforme figura, de modo que o comprimento do percurso [tex]ABPA[/tex] seja a metade do comprimento total da pista.
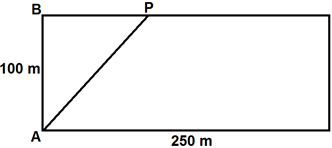
Qual a distância entre os pontos [tex]B[/tex] e [tex]P[/tex], em metros?
Solução 1
Como o comprimento do percurso [tex]ABPA[/tex] é a metade do comprimento total da pista, isto, é [tex]350[/tex] metros, obtemos a figura abaixo.
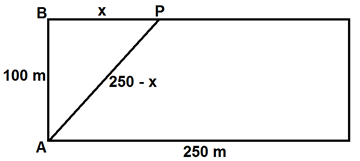
Aplicando o Teorema de Pitágoras no triângulo [tex]ABP[/tex], segue que:
[tex]\qquad x^2+100^2=(250-x)^2[/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$x=105 \, m$} \, .[/tex]
Assim, a distância entre os pontos [tex]B[/tex] e [tex]P[/tex] é de [tex]105[/tex] metros.
Solução elaborada pelos Moderadores do Blog.
Solução 2
Vamos determinar o comprimento total da pista que corresponde ao perímetro do retângulo da figura:
[tex]\qquad 2P=2\times100+2\times250=700 \, m[/tex].
A distância [tex]ABPA[/tex], que é o perímetro do triângulo [tex]ABP[/tex], é a metade do perímetro do retângulo, ou seja, igual a [tex]350 \, m[/tex].
Daí, percebemos que [tex]PB+PA = 350-100=250 \, m[/tex], então [tex]PA=250-PB.[/tex]
O triângulo [tex]ABP[/tex] é retângulo, então [tex](PA)^2 =(PB)^2 + (AB)^2[/tex] e substituindo o valor de [tex]PA[/tex] temos que:
[tex]\qquad \boxed{(250-PB)^2=PB^2+100^2}[/tex].
Desenvolvendo essa última igualdade, segue que:
[tex]\qquad 62500-500PB+PB^2=PB^2+10000[/tex].
[tex]\qquad 500PB=52500[/tex]
[tex]\qquad \boxed{PB=105 \, m} \, .[/tex]
Solução elaborada pelo Clube Deltonautas.
Participou da discussão o Clube Deltonautas.
