Problema
(Indicado a partir do 9º ano do E. F.)
Em um triângulo são traçadas duas cevianas[tex]^*[/tex], conforme mostrado na figura.
Calcule o valor de [tex]x+y[/tex].
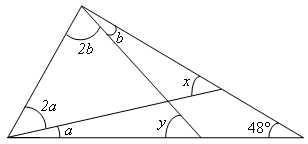
(*) Uma ceviana de um triângulo é um segmento de reta com uma extremidade em um vértice desse triângulo e a outra em um ponto qualquer da reta suporte do lado oposto a esse vértice.

Lembrete
✐ A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex]. (Se precisar, visite esta página.)
Solução 1
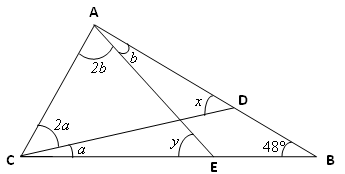
A soma dos ângulos internos do triângulo [tex]ABC[/tex] é [tex]180^{\circ}[/tex], assim:
[tex]\qquad 3b+48^{\circ}+3a=180^{\circ}[/tex]
[tex]\qquad 3(a+b)=180^{\circ}-48^{\circ}[/tex]
[tex]\qquad 3(a+b)=132^{\circ}[/tex]
[tex]\qquad \boxed{a+b=44^{\circ}} \, . \qquad \textcolor{#800000}{(i)}[/tex]
Como as somas dos ângulos internos dos triângulos [tex]ADC[/tex] e [tex] AEC[/tex] também são iguais a [tex]180^{\circ}[/tex], temos que:
[tex]\qquad 3b+x+2a=180^{\circ}[/tex]
[tex]\qquad 2b+y+3a=180^{\circ}[/tex]
e, com isso, somando essas duas equações, segue que:
[tex]\qquad 5b+x+y+5a=360^{\circ}[/tex]
[tex]\qquad x+y+5(a+b)=360^{\circ}[/tex]
[tex]\qquad x+y+5\times 44^{\circ}\stackrel{\textcolor{#800000}{(i)}}{=}360^{\circ}[/tex]
[tex]\qquad x+y+220^{\circ}=360^{\circ}[/tex]
[tex]\qquad x+y=360^{\circ}-220^{\circ}[/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$x+y=140^{\circ}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Sabemos que a soma dos ângulos internos de qualquer triângulo é [tex]180°[/tex].
Do triângulo grande vem [tex]3a+3b+48=180°[/tex]; daí [tex]3a+3b=132°[/tex], ou seja, [tex]a+b=44°[/tex].
No triângulo de ângulos [tex]2a[/tex] e [tex]2b[/tex], calculamos o terceiro ângulo ([tex]z[/tex]) usando a mesma relação.
[tex]\qquad 2a+2b+z=180°[/tex]
[tex]\qquad 2(a+b)+z=180°[/tex]
Sabemos que [tex]a+b=44°[/tex], então:
[tex]\qquad 2\times44+z=180°[/tex]
[tex]\qquad z=92°[/tex].
Observamos que o quadrilátero da figura tem ângulos de medidas [tex]92°[/tex] (opv), [tex]180°-x[/tex] (suplementar), [tex]180°-y[/tex] (suplementar) e [tex]48°[/tex].
Como sabemos que a soma dos ângulos internos de um quadrilátero é [tex]360°[/tex], vem:
[tex]\qquad 92°+(180°-x)+(180°-y)+48°=360°[/tex]
[tex]\qquad x+y=140°[/tex].
Solução elaborada pelo Clube Deltonautas, com contribuições dos Moderadores do Blog.
