Problema
(Indicado a partir do 9º ano do E. F.)
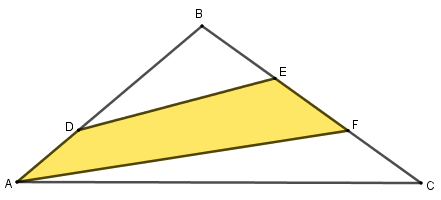
Na figura seguinte, o segmento [tex]AD[/tex] mede um terço do comprimento do segmento [tex]AB[/tex] e os pontos [tex]E \, [/tex] e [tex] \, F[/tex] dividem o lado [tex]BC[/tex] em três partes iguais.
Sabendo que a área do triângulo [tex]ABC[/tex] é [tex]9 \, cm^2[/tex], qual é a área do quadrilátero [tex]ADEF[/tex]?
Solução
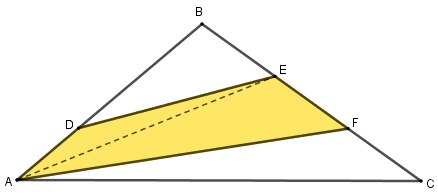
- Os dados do problema não permitem identificar o tipo do quadrilátero [tex]ADEF[/tex], então vamos dividi-lo em dois triângulos, traçando o segmento [tex]AE[/tex]. Dessa forma, observamos que a área do quadrilátero [tex]ADEF[/tex] é a soma das áreas dos triângulos [tex]EAD[/tex] e [tex]AEF[/tex].
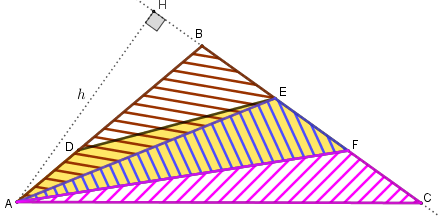
- Perceba que os triângulos [tex]ABE[/tex], [tex]AEF[/tex] e [tex]AFC[/tex] têm a mesma área, já que a altura de cada um deles é o segmento [tex]AH[/tex] de comprimento [tex]h[/tex] que aparece na próxima figura e a base de cada um é igual a um terço do segmento [tex]BC[/tex], pois os pontos [tex]E \, [/tex] e [tex] \, F[/tex] dividem o lado [tex]BC[/tex] em três partes iguais.
Assim, em particular, a área do triângulo [tex]AEF[/tex] que nos interessa é um terço da área do triângulo externo [tex]ABC[/tex], ou seja, [tex]\fcolorbox{black}{#eee0e5}{$S_{AEF}=\dfrac{1}{3}\cdot 9=3 \, cm^2$} \, .[/tex]
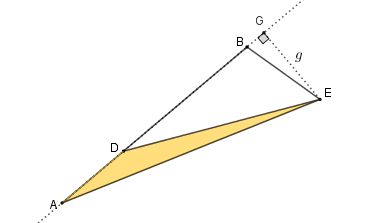
- Já temos a área do triângulo [tex]AEF[/tex]; precisamos, agora, determinar a área do triângulo [tex]EAD[/tex]. Para isso, observe pela figura abaixo que, como o segmento [tex]AD[/tex] mede um terço do comprimento do segmento [tex]AB[/tex], se considerarmos o segmento [tex]EG[/tex] de comprimento [tex]g[/tex] como a altura dos triângulos [tex]EAD[/tex] e [tex]ABE[/tex] relativa aos lados [tex]AD[/tex] e [tex]AB[/tex], respectivamente, então podemos concluir que a área do triângulo [tex]EAD[/tex] é um terço da área do triângulo [tex]ABE[/tex].
Como a área do triângulo [tex]ABE[/tex] é também [tex]3 \, cm^2[/tex], a área do triângulo [tex]EAD[/tex] será igual a [tex]\fcolorbox{black}{#eee0e5}{$S_{EAD}=\dfrac{1}{3}\cdot 3=1 \, cm^2$} \, .[/tex] - Finalmente, a área do quadrilátero [tex]ADEF[/tex] é dada por [tex]\fcolorbox{black}{#eee0e5}{$S_{ADEF}=S_{AEF}+S_{EAD}=3+1=4 \, cm^2$} \, [/tex].
Solução elaborada pelos Moderadores do Blog.
