✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
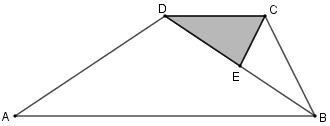
Sejam [tex]ABCD[/tex] um trapézio e [tex]E[/tex] o ponto médio da diagonal [tex]\overline{DB}[/tex].
Sabendo que o lado [tex]\overline{AB}[/tex] tem o triplo do comprimento do lado [tex]\overline{DC}[/tex] e que o trapézio [tex]ABCD[/tex] tem área [tex]24 \, cm^2[/tex], qual é a área do triângulo [tex]CDE[/tex]?
Notações
– Denotaremos o segmento definido por dois pontos genéricos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].
– A área de um objeto geométrico será indicada pela letra [tex]S[/tex], indexada com o nome do objeto: [tex]S_{\text{nome}}[/tex].
Solução
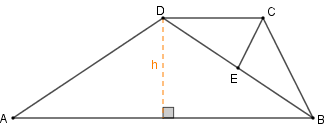
Vamos observar as áreas dos triângulos [tex]BCD[/tex] e [tex]ABD[/tex]:
[tex]\qquad S_{BCD}=\dfrac{DC \times h}{2} \qquad \qquad S_{ABD}=\dfrac{AB\times h}{2}.[/tex]
Como [tex]AB=3DC[/tex], então:
[tex] \qquad S_{ABD}=\dfrac{3DC\times h}{2}=3\cdot\dfrac{DC\times h}{2}=3\cdot S_{BCD} \, [/tex],
ou seja, a área do triângulo [tex]ABD[/tex] é o triplo da área do triângulo [tex]BCD.[/tex]
Por outro lado, a área do trapézio [tex]ABCD[/tex] é a soma das áreas dos triângulos [tex]BCD[/tex] e [tex]ABD[/tex], assim:
[tex]\qquad S_{ABCD}=S_{BCD}+S_{ABD}[/tex]
[tex]\qquad 24=S_{BCD}+3\cdot S_{BCD}[/tex]
[tex]\qquad 24=4\cdot S_{BCD}[/tex]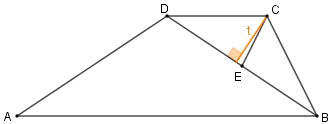
[tex]\qquad S_{BCD}=6\,cm^2.[/tex]
Observe agora que [tex]E[/tex] é o ponto médio da diagonal [tex]\overline{DB}[/tex]; assim, [tex]DB=2\cdot DE[/tex]
e dessa forma:
[tex]\qquad S_{CDE}=\dfrac{DE \cdot t}{2}=\dfrac{\dfrac{DB}{2}\cdot t}{2}=\dfrac{1}{2} \, \dfrac{DB\cdot t}{2}=\dfrac{1}{2}S_{BCD}=\dfrac{6}{2}=3.[/tex]
Assim, a área do triângulo [tex]CDE[/tex] é [tex]\,\fcolorbox{black}{#eee0e5}{$3\,cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
