Problema
(Indicado a partir do 9º ano do E. F.)
No jogo eletrônico Pac-Man, o personagem principal é descrito por uma cabeça redonda com uma boca que abre e fecha, seguidamente, para comer pastilhas espalhadas em labirintos.
1) Para pausar animação, basta clicar no ícone || que aparece no canto inferior esquerdo do aplicativo durante a animação.
2) Para reiniciar a animação, clique no ícone ► que irá aparecer no canto inferior esquerdo do aplicativo quando este estiver pausado.
Observe que, com a boca aberta, o corpo do personagem fica descrito por um setor circular.
A figura abaixo mostra um Pac-Man definido por um círculo de raio [tex]1 \, cm[/tex] e com a boca aberta segundo um ângulo de [tex]60^\circ[/tex].

Qual o comprimento, em centímetros, do contorno da região amarela que dá forma ao corpo do personagem mostrado na figura?

Sugestões
Na realidade, o Pac-Man é uma figura na qual visualizamos dois setores circulares: o, digamos, corpo, é um setor circular maior e, a boca, define um setor circular menor.
Solução
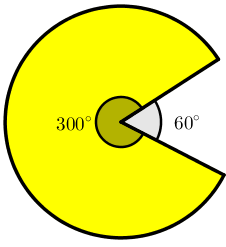
Olhando a figura, podemos perceber que é um setor circular menor, cuja medida é [tex]60^\circ[/tex], que dá forma à boca aberta do Pac-Man. Por outro lado, sabemos que a medida angular de uma circunferência é [tex]360^\circ[/tex]; assim, a parte amarela mostrada na figura corresponde a um setor circular maior, cuja medida é [tex]360^\circ – 60^\circ= 300^\circ[/tex].
Para encontrar o comprimento do contorno solicitado na questão (que matematicamente corresponde ao perímetro de um setor circular de [tex]300^\circ[/tex] definido em uma circunferência de raio unitário), precisamos apenas determinar o comprimento do arco que define o setor circular amarelo, já que temos o comprimento dos raios que dão formato à boca do personagem.
Como circunferências de raio unitário têm perímetros [tex]2\pi[/tex], uma regra de três simples nos ajuda a determinar o comprimento de arco necessário. Neste caso, se [tex]c[/tex] é o comprimento em questão, teremos:
| [tex]360^\circ[/tex] | ————————————– | [tex]2\pi \, cm[/tex] |
| [tex]300^\circ[/tex] | ————————————– | [tex]c[/tex] |
Assim, resulta que
[tex]\qquad c=\dfrac{300^\circ \cdot 2\cdot \pi}{360^\circ}=\dfrac{\cancel{300^\circ} \cdot 2\cdot \pi}{\cancel{360^\circ}}=\dfrac{\cancel{20} \cdot \pi}{\cancel{12}}=\dfrac{5 \cdot \pi}{3}[/tex]
ou seja, o arco em questão tem [tex]\dfrac{5}{3}\pi \, cm[/tex].
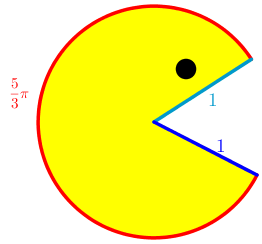
Dessa forma, o contorno do corpo do personagem terá comprimento de [tex]\fcolorbox{black}{#FFFF00}{$2+\dfrac{5}{3}\pi$}[/tex] centímetros.
Solução elaborada pelos Moderadores do Blog.
Para assistir, é só clicar na setinha.
