Problema
(Indicado a partir do 3º ano do E. M.)
Uma circunferência, com centro no primeiro quadrante, passa pelos pontos com coordenadas [tex](0, 0)[/tex] e [tex](4, 0)[/tex] e é tangente, internamente, à circunferência cuja equação é [tex]x^2+y^2=25[/tex].
Abaixo, estão ilustradas as duas circunferências.
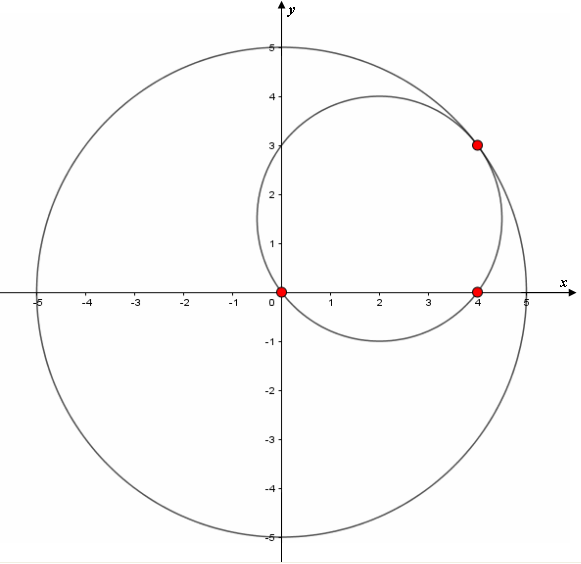
Determine as coordenadas do ponto de interseção dessas circunferências.
Lembrete
Nas soluções apresentadas, utilizou-se o seguinte fato:
✐ Se duas circunferências distintas são tangentes internas e a circunferência interna passa pelo centro da externa, então o segmento entre o centro da circunferência externa e o ponto de tangência é um diâmetro da circunferência interna.
Solução 1
Sejam [tex]C=(a,b)[/tex] e [tex]r[/tex] o centro e o raio, respectivamente, da circunferência interna. Observe que, como o centro está no primeiro quadrante, os valores de [tex]a[/tex] e [tex]b[/tex] devem ser positivos.
Na circunferência com equação [tex]x^2+y^2=25[/tex], podemos observar que o centro é [tex]O=(0,0)[/tex] e o raio é [tex]R=5[/tex].
Observe que o diâmetro da circunferência menor é igual ao raio da circunferência maior; aí, podemos concluir então que [tex]r=\frac{R}{2}=\frac{5}{2}[/tex]. Dessa forma, a equação da circunferência menor fica assim definida: [tex](x-a)^2+(y-b)^2=\frac{25}{4}[/tex]. Essa circunferência passa pelos pontos [tex](0,0)[/tex] e [tex](4,0)[/tex]; portanto, substituindo as coordenadas desses pontos na equação da circunferência, obtemos:
[tex]\qquad \begin{cases}
a^2+b^2=\frac{25}{4}\\
(4-a)^2+b^2=\frac{25}{4}
\end{cases}.[/tex]
Resolvendo esse sistema e considerando que [tex]a>0[/tex] e [tex]b>0[/tex], obtém-se [tex]a=2[/tex] e [tex]b=\frac{3}{2}[/tex].
Podemos então escrever a equação da circunferência tangente interna como [tex](x-2)^2+\left(y-\frac{3}{2}\right)^2=\frac{25}{4}.[/tex]
Finalmente, vamos encontrar o ponto de tangência das circunferências, [tex]T=(m,n)[/tex], e podemos fazer isso de duas maneiras.
- Como o ponto de tangência pertence às duas circunferências as coordenadas [tex](m,n)[/tex] desse ponto podem ser obtidas com a resolução do seguinte sistema:
- Mas, podemos calcular o ponto de tangência das circunferências de forma mais simples, observando que o ponto de tangência também pertence à reta definida pela equação [tex]y=\frac{3}{4}x.[/tex] (Reta que passa no ponto [tex](0,0)[/tex] e pelo centro [tex]\left(2, \frac{3}{2}\right)[/tex].)
[tex]\qquad \begin{cases}
m^2+n^2=25\\
(m-2)^2+\left(n-\frac{3}{2}\right)^2=\frac{25}{4}
\end{cases}.[/tex]
Então, para encontrarmos as coordenadas [tex](m,n)[/tex] do ponto de tangência, bastaria resolver o sistema:
[tex]\qquad \begin{cases}
n=\frac{3}{4}m\\
m^2+n^2=25
\end{cases}.[/tex]
De qualquer forma, obtemos [tex]m=4[/tex] e [tex]n=3.[/tex]
Logo, o ponto de tangência é [tex]\fcolorbox{black}{#eee0e5}{$T=(4,3)$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
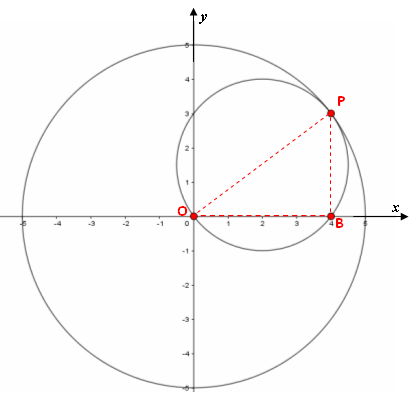Considere [tex]O= (0,0)[/tex], [tex]B=(4,0)[/tex] e [tex]P=(x_P,y_P)[/tex], o ponto de tangência das circunferências, em que [tex]x_P>0[/tex] e [tex]y_P>0[/tex] pois [tex]P[/tex] está no primeiro quadrante.
Assim, como [tex]\hat{OBP}[/tex] está inscrito em uma semicircunferência de diâmetro [tex]OP[/tex], temos que ele é um ângulo reto.
Como [tex]OB[/tex] é perpendicular a [tex]BP[/tex] e [tex]OB[/tex] é horizontal, temos que [tex]BP[/tex] é vertical e portanto [tex]B[/tex] e [tex]P[/tex] possuem mesma abscissa. Logo, [tex]x_P=4[/tex].
Por outro lado, [tex]P=(x_P,y_p)[/tex] é um ponto da circunferência de equação [tex]x^2+y^2=25[/tex], assim:
[tex]\qquad x_P^2+y_P^2=25 [/tex]
[tex]\qquad 4^2+y_P^2=25[/tex]
[tex]\qquad y_P=3.[/tex]
Portanto, o ponto de tangência é [tex]\fcolorbox{black}{#eee0e5}{$P=(4,3)$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.