As 7 pontes de Königsberg
Königsberg (atual Kaliningrado), na Prússia, era cortada pelo Rio Prególia, onde havia duas ilhas, que formavam um complexo que continha [tex]7[/tex] pontes. Naquele tempo, era discutida a possibilidade de se atravessar todas as pontes, sem repetir nenhuma. Em [tex]1736[/tex], Leonhard Euler provou que isso era impossível.
Primeiro, Euler retirou do problema tudo que não interessava. Ele transformou tudo num grafo:
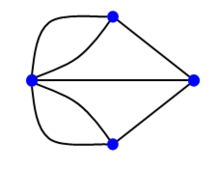
Observe que Euler transformou as pontes em segmentos de reta e em curvas e as ilhas em vértices. As retas e as curvas são como as pontes entre os vértices. Agora o desafio dele era percorrer as sete linhas, saindo de um desses quatro vértices e terminando também em um vértice. Era como percorrer todas as linhas sem tirar o lápis do papel.
Euler percebeu que, ao iniciar ou terminar a viagem em um vértice, se gastava uma linha, para sair ou para entrar. E para percorrer um dos outros vértices, ou o primeiro ou o último de novo (se possível, caso houvesse mais linhas), se gastava duas linhas, uma para sair e outra para entrar. Então dois vértices (ou nenhum vértice, se o percurso começar e terminar no mesmo vértice) deveriam estar ligado a um número ímpar de linhas, e os outros deveriam estar ligados a um número par de linhas. Mas no grafo das setes pontes de Königsberg não tinha sequer um vértice ligado a um número par de linhas.
Esse raciocínio de Euler não contribuiu só para desmentir a lenda de que era possível atravessar todas essas pontes, sem repetir nenhuma, mas nos dias de hoje é utilizado para resolver o mesmo tipo de problema, usando o mesmo tipo de lógica.
Bruno Barros de Sousa
aluno do PIC – OBMEP

