Problema
(Indicado a partir do 9º ano do E. F.)
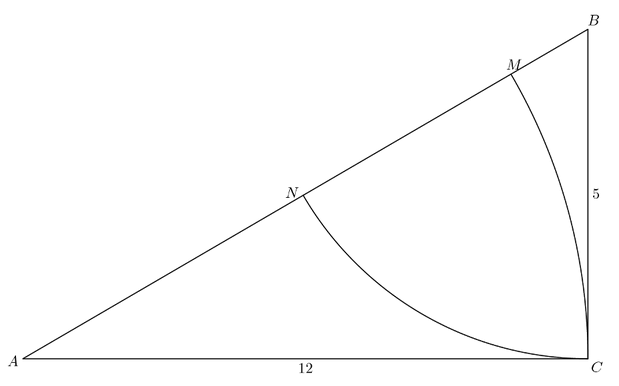
No triângulo retângulo [tex]ABC[/tex] da figura abaixo com catetos de comprimento [tex]5 \, cm[/tex] e [tex]12 \, cm[/tex], são traçados dois arcos de circunferência. Um deles com centro em [tex]A[/tex] e contendo [tex]C[/tex], outro com centro em [tex]B[/tex] e, também, contendo [tex]C[/tex]. Eles intersectam a hipotenusa nos pontos [tex]M[/tex] e [tex]N[/tex], respectivamente.
Qual o comprimento de [tex]\overline {MN}[/tex]?
Notação
Dado um segmento definido por dois pontos genéricos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], denotaremos o segmento por [tex]\overline {XY} [/tex] e o comprimento do segmento por [tex]XY[/tex].
Solução
Com os dados do problema, podemos obter os comprimentos de alguns segmentos mostrados na figura. Vejamos.
- Pelo Teorema de Pitágoras, temos que
[tex]\qquad AB=\sqrt{AC^2+BC^2}=\sqrt{12^2+5^2}=\sqrt{144+25}=\sqrt{169}=13.[/tex]
Assim, [tex]\boxed{AB=13 \, cm}.[/tex] - Como [tex]\overline {AM}[/tex] e [tex]\overline {AC} [/tex] são raios do mesmo círculo, então [tex]AM=AC=12 \, cm[/tex].
Com isso, [tex]MB=AB-AM=13-12=1[/tex], ou seja, [tex]\boxed{MB=1 \, cm}.[/tex] - [tex]\overline {BN}[/tex] e [tex]\overline {BC}[/tex] são raios de um mesmo círculo, logo [tex]BN=BC=5[/tex]. Assim, [tex]\boxed{BN=5 \, cm}[/tex]
Dessa forma, temos que:
[tex]\qquad \qquad MN=BN-BM=5-1=4[/tex],
ou seja, [tex]\fcolorbox{black}{#eee0e5}{$MN=4 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
