Problema
(Indicado a partir do 2º ano do E. M.)
O conjunto [tex]\{3,6,9,10\}[/tex] é acrescido de um quinto elemento, denotado por [tex]n[/tex] e diferente de todos os quatro elementos iniciais. Esse novo elemento faz com que a mediana dos elementos do conjunto recém-formado seja igual à sua média.
Qual é a soma de todos os possíveis valores de [tex]n[/tex]?

CONVITE:
Se você não se lembra do que é uma média, ou uma mediana, faça uma visita a esta SALA e, depois, mãos a obra!!
Solução
O conjunto [tex]\{3,6,9,10,n\}[/tex] possui um número ímpar de elementos, já que [tex]n \ne 3,6,9,10[/tex], logo a mediana é o elemento central que faz com que exatamente metade dos elementos do conjunto sejam menores do que ele e a outra metade seja maior. Assim, temos três possibilidades: ou a mediana é [tex]6[/tex], ou a mediana é [tex]9[/tex], ou [tex]n[/tex], dependendo do valor de [tex]n[/tex], conforme podemos visualizar na imagem abaixo.
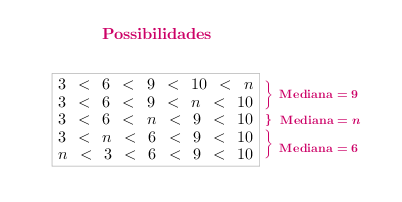
Vamos analisar cada caso, lembrando que, independente do valor de [tex]n[/tex], a média dos elementos do conjunto [tex]\{3,6,9,10,n\}[/tex] é dada por [tex]\boxed{\frac{3+6+9+10+n}{5}}[/tex].
- Se a mediana for [tex]6[/tex], como a média é igual à mediana, teremos [tex]\dfrac{3+6+9+10+n}{5} = 6[/tex] e, assim, [tex]\boxed{n = 2}[/tex].
- Analogamente, se a mediana for [tex]9[/tex], teremos [tex]\dfrac{3+6+9+10+n}{5} = 9[/tex] e, então, [tex]\boxed{n = 17}[/tex].
- Por fim, se a mediana for [tex]n[/tex], então [tex]\dfrac{3+6+9+10+n}{5} = n[/tex] e, agora, [tex]\boxed{n = 7}[/tex].
A soma de todas as possibilidades nos dá, então, [tex]\fcolorbox{black}{#eee0e5}{$2 + 7 + 17 = 26$}[/tex].
Solução elaborada pelos Moderadores do Blog.
