Problema
(Indicado a partir do 2º ano do E. M.)
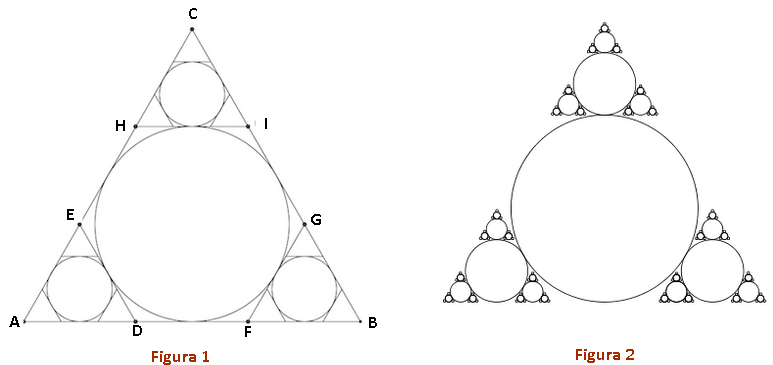
(UFPA-2005 Modificada) A Figura 2 abaixo é comumente reconhecida como um “fractal” (onde pequenas partes são cópias reduzidas do todo) e é constituída por uma infinidade de círculos de raios cada vez menores. Sua construção é dada a seguir.
A partir de um triângulo equilátero [tex]ABC[/tex], cujo lado tem comprimento [tex]L[/tex], considere a circunferência nele inscrita.
- A reta paralela ao lado [tex]\overline{BC}[/tex] e tangente à circunferência inscrita intersecta o lado [tex]\overline{AB}[/tex] no ponto [tex]D[/tex] e o lado [tex]\overline{AC}[/tex] no ponto [tex]E[/tex], formando um novo triângulo equilátero [tex]ADE.[/tex]
- Fazendo construções equivalentes para os lados [tex]\overline{AC}[/tex] e [tex]\overline{AB}[/tex], determinaremos dois novos triângulos equiláteros [tex]BFG[/tex] e [tex]CHI.[/tex]
- Para cada um dos triângulos [tex]ADE[/tex], [tex]BFG[/tex] e [tex]CHI[/tex], repetimos o processo acima, obtendo três novas circunferências inscritas e nove triângulos menores.
Esse processo pode ser repetido indefinidamente, gerando círculos cada vez menores e formando a Figura 2.
(a) Mostre que o raio do círculo inscrito num triângulo equilátero é igual a um terço da altura do triângulo.
(b) Calcule a área do primeiro círculo construído e a área de um dos círculos menores da Figura 1, em função do lado [tex]L[/tex] do triângulo inicial.
(c) Determine a soma das áreas dos círculos congruentes gerados na etapa [tex]n[/tex].
(d) As somas das áreas dos círculos congruentes (de mesmo raio), em ordem decrescente, formam uma progressão geométrica. Calcule a soma dos infinitos termos dessa progressão.
Lembretes
Alguns resultados de geometria plana:
[tex] \color{#800000}{(i)}[/tex] Dados um ponto e uma reta, existe apenas uma reta que passa pelo ponto e é perpendicular à reta dada.
[tex] \color{#800000}{(ii)}[/tex] O raio traçado até o ponto de tangência é perpendicular à reta tangente.
[tex] \color{#800000}{(iii)}[/tex] Em um triângulo equilátero, a mediana, a altura e a bissetriz interna relativas ao mesmo lado coincidem.
Solução
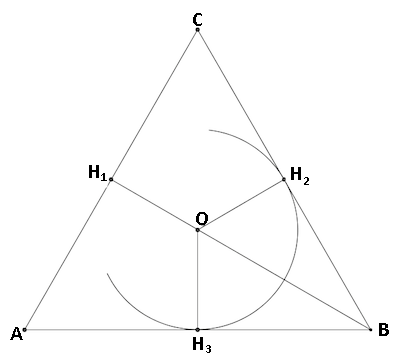(a) Considere um triângulo equilátero [tex]ABC[/tex] de lado medindo [tex]L[/tex]. Na figura ao lado, mostramos parte da circunferência inscrita a esse triângulo, bem como o centro [tex]O[/tex] e dois pontos de tangência [tex]H_2[/tex] e [tex]H_3[/tex] da circunferência com os lados [tex]\overline{BC}[/tex] e [tex]\overline{AB}[/tex], respectivamente. O ponto [tex]H_1[/tex] é a interseção da semirreta [tex]BO[/tex] com [tex]\overline{AC}[/tex].
Devido a [tex] \color{#800000}{(ii)}[/tex] temos que [tex]B\hat{H_2}O[/tex] e [tex]B\hat{H_3}O[/tex] são ângulos retos. Deste modo os triângulos [tex]BH_2O[/tex] e [tex]BH_3O[/tex] são congruentes (triângulos retângulos que possuem ordenadamente congruentes a hipotenusa e um cateto), e concluímos que [tex]O\hat{B}H_2 \cong O\hat{B}H_3[/tex], ou seja, [tex]BO[/tex] é bissetriz de [tex]A\hat{B}C[/tex].
Assim, [tex]\overline{BH_1}[/tex] é bissetriz interna do triângulo e, por [tex] \color{#800000}{(iii)}[/tex], também é mediana e altura. Sendo [tex]\overline{BH_1}[/tex] mediana, concluímos que [tex]H_1[/tex] é ponto médio de [tex]\overline {AC}[/tex].
Sendo [tex]\overline{BH_1}[/tex] altura, temos que [tex]H_1[/tex] é o ponto de tangência da circunferência com [tex]\overline{AC}[/tex], caso contrário teríamos duas perpendiculares à reta [tex]AC[/tex] traçada por [tex]O[/tex] (contrariando [tex] \color{#800000}{(i)}[/tex]).
Assim, num triângulo equilátero a circunferência inscrita tangencia cada lado no ponto médio.
Indicando por [tex]h[/tex] a medida da altura do triângulo equilátero e aplicando o teorema de Pitágoras no triângulo [tex]ABH_1[/tex], segue que
[tex]\qquad L^2 = h^2 + \left(\dfrac{L}{2}\right)^2[/tex]
[tex]\qquad h^2 = L^2 – \dfrac{L^2}{4}[/tex]
[tex]\qquad h^2 = \dfrac{3L^2}{4}[/tex]
[tex]\qquad h = \dfrac{L \sqrt{3}}{2}[/tex]. [tex] \qquad \color{#800000}{(*)}[/tex]
Perceba que os triângulos [tex]BOH_2[/tex] e [tex]BCH_1[/tex] são semelhantes (pelo caso AA). Sendo [tex]r[/tex] a medida do raio da circunferência inscrita, temos que [tex]\dfrac{r}{\dfrac{L}{2}} = \dfrac{\dfrac{L}{2}}{h}[/tex], ou seja, [tex] r = \dfrac{\dfrac{L^2}{4}}{h}[/tex].
Assim, usando [tex] \color{#800000}{(*)}[/tex], segue que:
[tex]\qquad r=\dfrac{\dfrac{L^2}{4}}{h} \stackrel{\textcolor{#800000}{(*)}}{=} \dfrac{\dfrac{L^2}{4}}{\dfrac{L \sqrt{3}}{2}} = \dfrac{L}{2\sqrt{3}}=\dfrac{L\sqrt{3}}{6} \stackrel{\textcolor{#800000}{(*)}}{=} \dfrac{h}{3}[/tex].
(b) Seja [tex]A_n[/tex] a área de um círculo obtido em cada etapa [tex]n[/tex] da construção. Particularmente,
[tex]\qquad A_1 = \pi \cdot r^2 = \pi \cdot \left(\dfrac{L\sqrt{3}}{6}\right)^2 = \dfrac{3 \pi L^2}{36} = \dfrac{\pi}{12} L^2[/tex].
Os triângulos [tex]ADE[/tex], [tex]BFG[/tex] e [tex]CHI[/tex] são semelhantes ao triângulo [tex]ABC[/tex], já que, sendo obtidos por paralelas aos lados do triângulo [tex]ABC[/tex], terão os mesmos ângulos dele.
Perceba pelo item (a) que a altura dos triângulos pequenos será [tex]h – 2r = h – \dfrac{2h}{3} = \dfrac{h}{3}[/tex]. Assim, a razão de semelhança entre os triângulos será dada pela razão das alturas que é [tex]\dfrac{1}{3}[/tex] e, portanto, os círculos menores da Figura 1 têm como raio um terço do raio do círculo maior. Com isso:
[tex]\qquad A_2 = \pi \cdot \left(\dfrac{r}{3}\right)^2 = \dfrac{1}{9} \cdot A_1 = \dfrac{\pi}{108} L^2[/tex]
Podemos generalizar, afirmando que um círculo obtido na etapa [tex]n + 1[/tex] terá sempre [tex]\dfrac{1}{9}[/tex] da área de um círculo obtido na etapa [tex]n[/tex]. Ou seja, [tex](A_1,\, A_2,\, \ldots\,,A_n,\,\ldots)[/tex] é uma Progressão Geométrica de razão [tex]\dfrac{1}{9}[/tex].
(c) Seja [tex]C_n[/tex] o número de círculos congruentes gerados na etapa [tex]n[/tex].
Perceba que cada círculo de uma etapa gera três círculos na etapa seguinte, ou seja, [tex](C_1,\, C_2,\, \ldots\,,C_n,\,\ldots)[/tex] é uma Progressão Geométrica de razão [tex]3[/tex].
Seja [tex]S_n[/tex] a soma das áreas dos círculos congruentes gerados na etapa [tex]n[/tex].
Temos [tex]S_n = C_n \cdot A_n = 3 \cdot C_{n-1} \cdot \dfrac{1}{9} \cdot A_{n-1} = \dfrac{1}{3} \cdot S_{n-1}[/tex], ou seja, [tex](S_1,\, S_2,\, \ldots\,,S_n,\,\ldots)[/tex] é uma Progressão Geométrica de razão [tex]\dfrac{1}{3}[/tex].
Portanto, a soma das áreas dos círculos gerados na etapa [tex]n[/tex] será obtida pela fórmula do termo geral da PG acima:
[tex]\qquad S_n = S_1 \cdot \left(\dfrac{1}{3}\right)^{n-1} = \dfrac{\pi}{12 \cdot 3^{n-1}}L^2[/tex]
(d) Basta utilizar a fórmula da soma dos termos de uma PG infinita cuja razão tem módulo menor do que [tex]1[/tex]:
[tex]\qquad S_1 + S_2 + \ldots = \dfrac{S_1}{1 – \dfrac{1}{3}} = \dfrac{3 S_1}{2} = \dfrac{3 A_1}{2} = \dfrac{3}{2} \cdot \dfrac{\pi}{12} L^2 = \dfrac{\pi}{8} L^2.[/tex]
Solução elaborada pelos Moderadores do Blog.