Problema
(Indicado a partir do 8º ano do E. F.)
O desenho mostra uma linha poligonal fechada e destaca alguns ângulos retos, além de três medidas angulares dadas em graus.
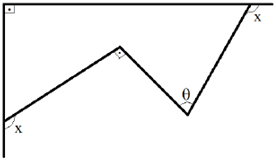
Sabendo que o ângulo [tex]\theta[/tex] é agudo, encontre o maior valor inteiro ímpar possível para [tex]x[/tex].
Solução
Tracemos a semirreta [tex]s[/tex] paralela à semirreta [tex]r[/tex], conforme mostra a figura. Assinalamos na mesma figura o ângulo de [tex]\textcolor{blue}{x-90^\circ}[/tex] definido por [tex]s[/tex] e o ângulo de [tex]\textcolor{red}{180^\circ-x}[/tex] definido por [tex]r[/tex].
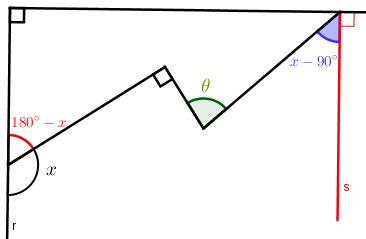
- A partir da figura acima, você conseguiria provar que [tex]\boxed{(180^\circ -x) +\theta=90^\circ +(x-90^\circ)}[/tex]?
Pois bem, após demonstrar isso é fácil chegar a [tex]\theta=2x-180^\circ[/tex].
Como [tex]\theta[/tex] é agudo, segundo o enunciado, então [tex]\theta \lt 90^\circ[/tex], ou seja, [tex]2x-180^\circ \lt 90^\circ[/tex].
Dessa forma, [tex]x\lt 135^\circ[/tex]; e, como queremos o maior valor ímpar e inteiro para [tex]x[/tex], temos [tex]\fcolorbox{black}{#eee0e5}{$ \, x=133^\circ \, $} \, [/tex].
Solução elaborada pelos Moderadores do Blog.
