Problema
(Indicado a partir do 1º ano do E. M.)
Noemi adoeceu e, ao ir ao médico, ele receitou um remédio cuja concentração na corrente sanguínea, em partes por milhão [tex](ppm)[/tex], após [tex]t[/tex] horas da sua ingestão, é dada pela função quadrática definida por
- [tex]C(t)=-t^2+8t[/tex], [tex]t\in[0,8][/tex].
Nessa função, considera-se [tex]t=0[/tex] o momento em que o paciente toma uma dose da medicação.
Noemi tomou a primeira dose às [tex]8[/tex] horas de uma sexta-feira, assim:
(a) Qual o dia e horário em que o medicamento atingirá, na corrente sanguínea da Noemi, [tex]12[/tex] [tex]ppm[/tex] pela primeira vez?
(b) Determine o dia e o horário que o médico deve prescrever para a ingestão da segunda dose da medicação, sabendo que o mesmo deverá ser tomado quando a concentração de medicamento na corrente sanguínea da Noemi for máxima.
(c) Considerando que a segunda dose foi tomada no horário estipulado no item (b), determine a concentração de medicamento na corrente sanguínea de Noemi uma hora após ingerida a segunda dose.

Lembretes
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
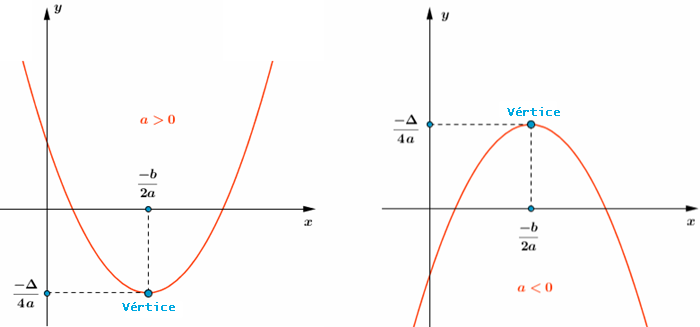
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a} \, [/tex] e [tex] \, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução 1
(a) Para encontrarmos o tempo transcorrido entre a primeira dose e o momento em que a concentração do medicamento na corrente sanguínea seja [tex]12[/tex] [tex]ppm[/tex], devemos obter os possíveis valores de [tex]t[/tex] para os quais [tex]C(t)=12[/tex].
Como [tex]\boxed{C(t)=-t^2+8t}[/tex], segue que [tex]12=-t^2+8t[/tex], ou ainda, [tex]t^2-8t+12=0[/tex].
Assim, precisamos obter as raízes da equação [tex]\boxed{t^2-8t+12=0}[/tex].
Para isso, calculamos [tex]\Delta[/tex]:
[tex]\qquad \Delta=8^2-4\times1\times 12[/tex]
[tex]\qquad \Delta=64-48[/tex]
[tex]\qquad \Delta=16[/tex]
e obtemos as soluções:
[tex]\qquad t=\dfrac{8\pm 4}{2}[/tex]
[tex]\qquad t=2[/tex] ou [tex]t=6[/tex].
Dessa forma, o menor tempo ocorre quando [tex]t=2[/tex] e isso significa que se passaram duas horas, desde que Noemi tomou a primeira dose da medicação. Podemos concluir, então, que isto aconteceu às [tex]10[/tex] horas da sexta-feira.
(b) Pelo Lembrete 2, para calcularmos o tempo decorrido até o medicamento atingir a concentração máxima no organismo da Noemi, basta calcularmos a coordenada "[tex]x_v[/tex]" do vértice da parábola; no nosso caso, [tex]t_v[/tex]:
[tex]\qquad t_v=- \dfrac{b}{2a}=- \dfrac{8}{-2}=4.[/tex]
Assim, a segunda dose deverá ser tomada passadas quatro horas da primeira dose, ou seja, às [tex]12[/tex] horas da sexta-feira.
(c) Como se passou uma hora desde que Noemi tomou a segunda dose, a concentração referente à essa dosagem é dada por:
[tex]\qquad C(1)=-1^2+8\times1=7[/tex] [tex]ppm[/tex].
Com relação à primeira dose, já se passaram cinco horas (quatro antes da segunda dose para ministrar a primeira e uma após a segunda dose). Desta forma a concentração de medicação no sangue de Noemi referente à primeira dose é dada por:
[tex]\qquad C(5)=-5^2+8\times5=15[/tex] [tex]ppm[/tex] .
Somando as duas concentrações temos, no sangue de Noemi, a concentração de [tex]7+15=22[/tex] [tex]ppm[/tex] de medicamento.
Solução elaborada pelos Moderadores do Blog.
Solução 2
a) Pede-se o horário em que a concentração do remédio na corrente sanguínea é de [tex]12 \, ppm[/tex], isso significa achar [tex]t[/tex] tal que [tex]-t^{2}+8t=12[/tex].
Resolvendo tal igualdade, temos que [tex]t=2[/tex] e [tex]t=6[/tex]. Logo, a primeira vez em que a concentração do remédio na corrente sanguínea atingirá [tex]12 \, ppm [/tex] será duas horas após a ingestão da primeira dose: às 10h da manhã de sexta.
b) A concentração do remédio na corrente sanguínea será máxima quando [tex]t=\dfrac{-b}{2a}=\dfrac{-8}{2(-1)}=4[/tex], isto é, quatro horas após a ingestão da primeira dose: meio-dia de sexta.
c) Seja [tex]C_{1}(t)=-t^{2}+8t \, [/tex] e [tex] \, C_{2}(t)=-(t-4)^{2}+8(t-4)[/tex], sendo [tex]C_{1}[/tex] a concentração da primeira dose e, [tex]C_{2}[/tex], a da segunda dose. Assim, uma hora após a segunda dosagem ser aplicada, isto é, [tex]t=5[/tex], a concentração do remédio na corrente sanguínea será de:
[tex]\quad C_{1}(5)+C_{2}(5)=-5^{2}+8\cdot5-1^{2}+8=48-26=22 \, ppm[/tex].
olução elaborada pelo Clube Paralelo 38 , com contribuições dos Moderadores do Blog.