Problema
(Indicado a partir do 1º ano do E. M.)
Uma empresa resolveu fazer seu logotipo conforme a figura abaixo.
Para tal, foi realizada uma proposta para a confecção de um painel a ser colocado na sede da empresa, utilizando o desenho abaixo, no qual cada circunferência é tangente ao retângulo do entorno em três pontos. O retângulo possui base [tex]3\;m[/tex] e altura [tex]2\;m.[/tex]
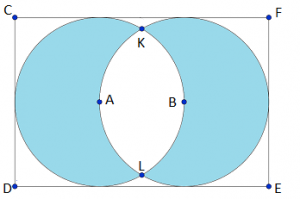
(a) As circunferências possuem o mesmo valor de raio? Justifique.
(b) Qual a medida do ângulo [tex]K\hat{A}L[/tex]?
(c) Calcule a área do logotipo construído (região destacada em azul na figura).
Solução
(a) Sim.
Como as circunferências são tangentes ao retângulo [tex]CDEF[/tex], temos que a altura desse retângulo equivale ao diâmetro de cada circunferência. Como possuem diâmetros iguais, então as circunferências possuem a mesma medida de raio.
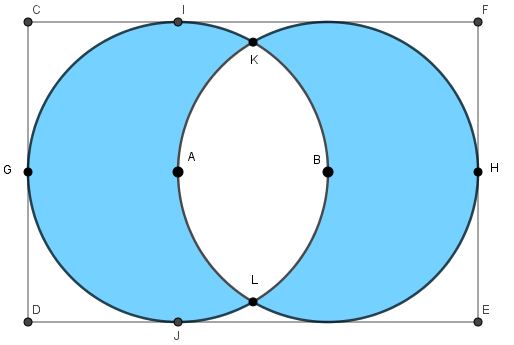
Particularmente, podemos obter o valor do raio de ambas:
[tex]\quad 2r=2 \\
\quad r=1\;m.[/tex]
(b) Observe que a circunferência esquerda passa pelo centro da circunferência direita e a circunferência direita passa pelo centro da circunferência esquerda, pois o comprimento do retângulo é [tex]3\;m[/tex], o que equivale exatamente à medida de três raios.
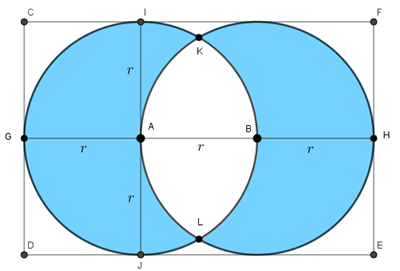
Observe também que os triângulos [tex]\triangle ABK[/tex] e [tex]\triangle ABL[/tex] são equiláteros, uma vez que seus lados medem [tex]r=1\;m[/tex]. Assim, os ângulos [tex]K\hat{A}B[/tex] e [tex]L\hat{A}B[/tex] valem [tex]60^\circ[/tex].
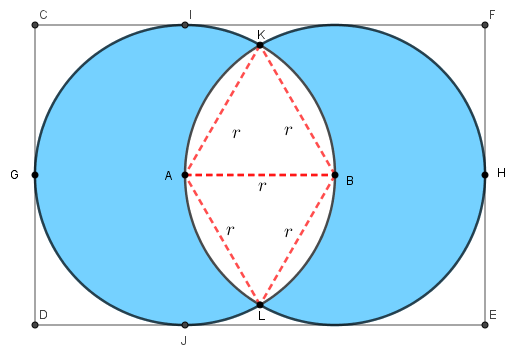
Portanto, [tex]K\hat{A}L=K\hat{A}B+ L\hat{A}B =60^\circ +60^\circ=120^\circ.[/tex]
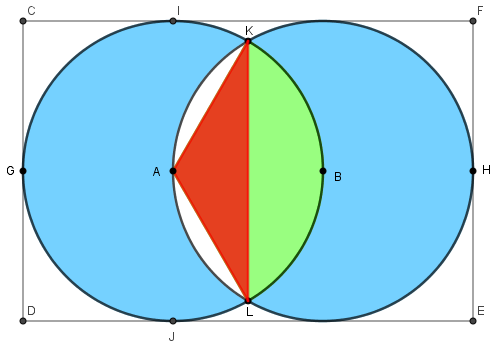
(c) Perceba que a área da região destacada em azul é a diferença entre "a área relativa às duas circunferências" e "duas vezes a área relativa à interseção das circunferências" (uma vez que devemos retirar a área da região branca de ambas as circunferências).
- A área [tex]A[/tex] (em [tex]m^2[/tex]) relativa às duas circunferências é o dobro da área de um círculo de raio [tex]r=1\;m[/tex]; assim:
[tex]\quad A=2\times\pi \times 1^2=2\pi[/tex]. - Para determinar a área relativa à interseção das duas circunferências, devemos inicialmente fazer a diferença entre a área do setor circular cujo ângulo central vale [tex]120^\circ[/tex] e a área do triângulo [tex]\triangle KAL[/tex]. Após encontrarmos o resultado (que é a área da região em verde na figura a seguir), multiplicamos por [tex]2[/tex].
- Cálculo da área do setor [tex]A_s[/tex]
Este cálculo pode ser realizado utilizando-se uma regra de três simples: - Existem várias maneiras de determinarmos a área do triângulo em vermelho. Podemos, por exemplo, traçar a altura referente à base [tex]KL[/tex] e decompor o triângulo vermelho em dois triângulos retângulos congruentes, cujos ângulos medem [tex]60^\circ[/tex] e [tex]30^\circ.[/tex] Observe que o cateto horizontal dos triângulos decompostos vale [tex]0.5\;m[/tex], uma vez que é a metade do raio, e a medida da hipotenusa é [tex]1\;m[/tex], uma vez que é a medida do raio das circunferências. O outro cateto (cuja medida denotaremos por [tex]l[/tex]) pode ser calculado usando o seno do ângulo [tex]60^\circ[/tex]:
[tex]\quad sen(60^\circ)=\dfrac{l}{1}\\
\quad l=\dfrac{\sqrt{3}}{2}.[/tex]
Assim, o triângulo em vermelho foi decomposto em dois triângulos retângulos cujos catetos medem [tex]\dfrac{1}{2}[/tex] e [tex]\dfrac{\sqrt{3}}{2}[/tex] e portanto a área [tex]A_t[/tex] do triângulo em vermelho (em [tex]m^2[/tex]) é dada por:
[tex]\quad A_t=2 \times \dfrac{\dfrac{1}{2}\times\dfrac{\sqrt{3}}{2}}{2}=\dfrac{\sqrt{3}}{4}[/tex]. - Finalmente, temos que a área da região destacada em azul (em [tex]m^2[/tex]) é dada por:
[tex]\quad A_l=2\pi-2A_v[/tex]
[tex]\quad A_l=2\pi-2(\dfrac{\pi}{3}-\dfrac{\sqrt{3}}{4})[/tex]
[tex]\quad A_l=2\pi-\dfrac{2\pi}{3}+\dfrac{\sqrt{3}}{2}[/tex]
[tex]\quad A_l=\dfrac{4\pi}{3}+\dfrac{\sqrt{3}}{2}.[/tex]
[tex]\begin{array}{c c c}
\textrm{Ângulo} && \textrm{Área} \\
360^\circ &-& \pi\\
120^\circ &-& A_s
\end{array}[/tex]
- Como as medidas em questão são diretamente proporcionais, podemos, então, concluir que [tex]A_s=\dfrac{120^\circ\times \pi}{360^\circ}[/tex], ou seja, [tex]A_s=\dfrac{\pi}{3} \; m^2[/tex].
Dessa forma, podemos concluir que a área [tex]A_v[/tex] da região verde vale:
[tex]\quad A_v=A_s-A_t=(\dfrac{\pi}{3}-\dfrac{\sqrt{3}}{4}) \; m^2[/tex].
Portanto, a área do logotipo construído é [tex]\boxed{\dfrac{4\pi}{3}+\dfrac{\sqrt{3}}{2}\; m^2}[/tex].
Solução elaborada pelos Moderadores do Blog.
