Problema
(Indicado a partir do 3º ano do E. M.)
Dado o tetraedro regular [tex]ABCD[/tex] com aresta medindo [tex]a[/tex], considere [tex]E[/tex] e [tex]F[/tex] pontos médios das arestas [tex]\overline{AC}[/tex] e [tex]\overline{BD}[/tex], respectivamente.
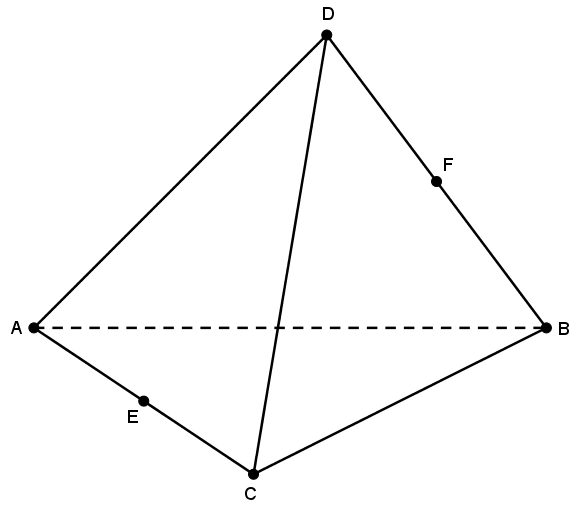
Determine a distância entre os pontos [tex]E[/tex] e [tex]F[/tex].
Solução
Observe o tetraedro abaixo, no qual traçamos os segmentos [tex]\overline{AF}[/tex] e [tex]\overline{CF}[/tex], bem como o segmento [tex]\overline{EF}[/tex].
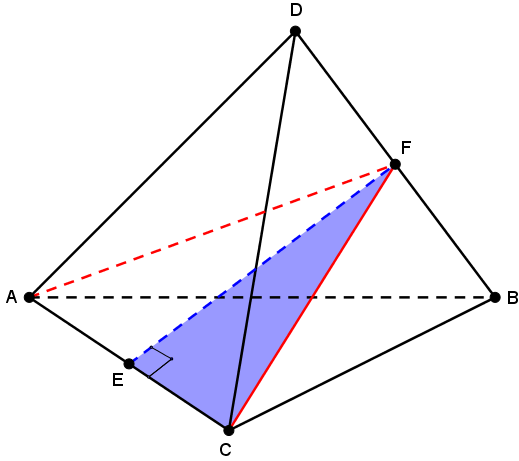
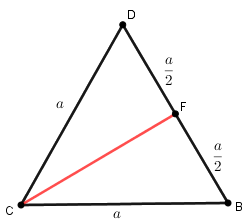
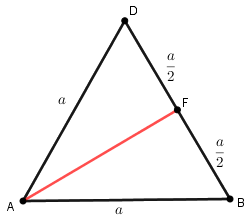
- Como o tetraedro é regular, suas faces são triângulos equiláteros; assim, na face [tex]BCD[/tex] o segmento [tex]\overline{CF}[/tex] é mediana e altura (e também bissetriz e mediatriz) e, com isso, [tex]BCF[/tex] e [tex]CFD[/tex] são triângulos retângulos. Portanto, temos que [tex]FD=\dfrac{a}{2}[/tex] e [tex]\boxed{CF=\dfrac{a\sqrt{3}}{2}}[/tex].
- De maneira análoga, se observarmos a face [tex]ABD[/tex], podemos concluir que o segmento [tex]\overline{AF}[/tex] é também uma mediana e altura e, então, [tex]\boxed{AF=\dfrac{a\sqrt{3}}{2}}[/tex].
- Note, agora, que [tex]AFC[/tex] é um triângulo isósceles, com [tex]AF=CF[/tex]; dessa forma, [tex]\overline{FE}[/tex] é mediana e altura com relação ao lado [tex]\overline{AC}[/tex].
Aplicando o Teorema de Pitágoras ao triângulo [tex]FEC[/tex], segue, finalmente, que:
[tex]\qquad (EF)^2+(EC)^2=(CF)^2[/tex]
[tex]\qquad (EF)^2=(CF)^2-(EC)^2[/tex]
[tex]\qquad (EF)^2=\left(\dfrac{a\sqrt{3}}{2}\right)^2-\left(\dfrac{a}{2}\right)^2[/tex]
[tex]\qquad (EF)^2=\dfrac{2a^2}{4}[/tex]
[tex]\qquad EF=\dfrac{a\sqrt{2}}{2}[/tex].
Logo, a distância entre os pontos [tex]E[/tex] e [tex]F[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{a\sqrt{2}}{2}$} \, [/tex] unidades de comprimento.
Solução elaborada pelos Moderadores do Blog.
