Problema
(Indicado a partir do 1º ano do E. M.)
Sobre os lados [tex]\overline{BC}[/tex] e [tex]\overline{CD}[/tex] de um retângulo [tex]ABCD[/tex], são marcados os seus respectivos pontos médios [tex]E[/tex] e [tex]F[/tex].
Em seguida, liga-se o ponto [tex]F[/tex] aos pontos [tex]A[/tex] e [tex]B[/tex] e o ponto [tex]E[/tex] aos pontos [tex]A[/tex] e [tex]D[/tex], determinando-se os segmentos [tex]\overline{FA}[/tex], [tex]\overline{FB}[/tex], [tex]\overline{EA}[/tex] e [tex]\overline{ED}[/tex].
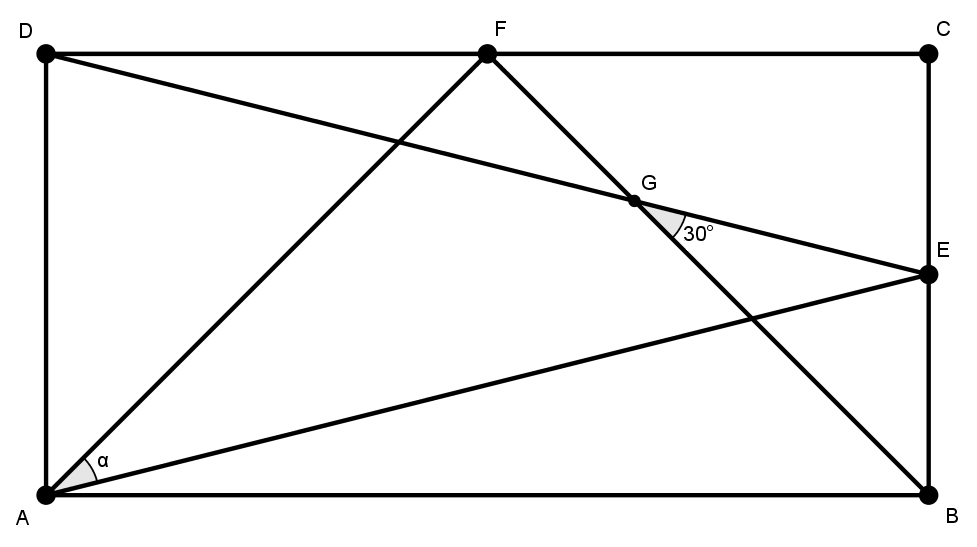
Dado que a medida do ângulo [tex]\angle{B{G}E}[/tex] é [tex]30^\circ[/tex], qual a medida [tex]\alpha[/tex] do ângulo [tex]\angle{E{A}F}[/tex] ?
Solução
Seja [tex]H[/tex] o ponto médio de [tex]\overline{AB}[/tex].
Considere os segmentos [tex]\overline{DH}[/tex] e [tex]\overline{DE}[/tex] e seja [tex]\beta[/tex] a medida do ângulo [tex]\angle{H{D}E}[/tex].
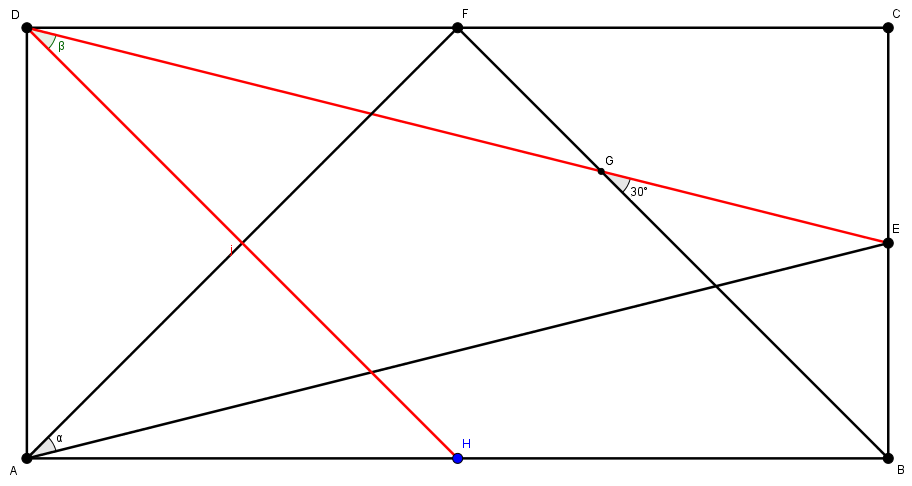
Observe que:
- Os ângulos [tex]\angle{H{D}E}[/tex] e [tex]\angle{F{A}E}[/tex] são congruentes (por que será?); assim, [tex]\alpha=\beta[/tex].
- [tex]\overline{DH}//\overline{FB}[/tex] (por que também?); logo, [tex]\beta=30^\circ[/tex].
Portanto, podemos concluir que [tex]\alpha=\beta=30^\circ[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se você não sabe o que são ângulos alternos e ângulos correspondentes, clique AQUI. |
