Problema
(Indicado a partir do 1º ano do E. M.)
Conforme dados obtidos pelo IBGE (Instituto Brasileiro de Geografia e Estatística) relativos às taxas de analfabetismo da população brasileira com 15 anos ou mais de idade, a partir de 1960, foi possível ajustar uma curva de equação [tex]y = 30 k^x + 10[/tex], na qual [tex]k \gt 0[/tex] é uma constante, [tex]x[/tex] indica quantos anos se passaram desde 1960 e [tex]y[/tex] é o valor da taxa, em porcentagem, num certo ano. Tal curva é representada a seguir.
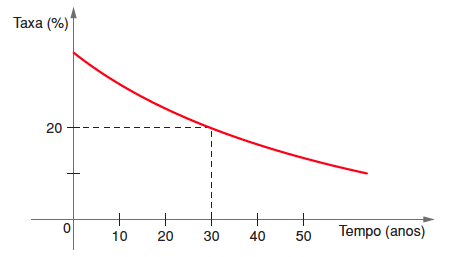
Usando o gráfico e a equação da curva, faça o que se pede:
(a) Determine o valor de [tex]k[/tex].
(b) Obtenha a taxa referente ao ano de 1960.
(c) Calcule uma estimativa de taxa para o ano de 2020.
Solução
(a) Pelo gráfico, vemos que para [tex]x=30[/tex] temos [tex]y=20[/tex], ou seja, [tex]20 = 30 k^{30} +10[/tex].
Assim, segue que:
[tex]\qquad 20 = 30 k^{30} +10 \\
\qquad k^{30} = \dfrac{1}{3}\\
\qquad \boxed{k =\sqrt[30]{\dfrac{1}{3}}}.[/tex]
(b) Em 1960, temos [tex]x = 0[/tex]; assim:
[tex]\qquad y = 30 \cdot \left( \sqrt[30]{\dfrac{1}{3}} \right)^0 + 10 [/tex].
Mas, como todo número não nulo elevado a zero é igual a um, segue que:
[tex]\qquad y= 30 \cdot 1 + 10 = 40[/tex].
Logo, a taxa de analfabetismo em 1960 foi de [tex]\boxed{40 \%}[/tex].
(c) Agora, queremos determinar o valor de [tex]y[/tex] quando [tex]x = 2020 – 1960 = 60[/tex].
Então:
[tex]\qquad y = 30 \cdot \left( \sqrt[30]{\dfrac{1}{3}} \right)^{60} + 10 = 30 \cdot \left(\dfrac{1}{3}\right)^2 + 10 = \dfrac{30}{9} + 10 \approx 13,33.[/tex]
Portanto, a estimativa para a taxa de analfabetismo em 2020 é de [tex]\boxed{13,33 \%}[/tex].
Solução elaborada pelos Moderadores do Blog.
