Problema
(Indicado a partir do 8º ano do E. F.)
Seja [tex]n[/tex] um inteiro positivo.
Qual é a soma dos dígitos do número [tex](10^{4n^2+8}+1)^2[/tex]?
Essa soma depende de [tex]n[/tex]?

Para ajudar. . .
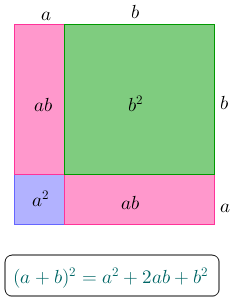
Você se lembra do produto notável “quadrado da soma”?
Você vai precisar dessa identidade algébrica para resolver o problema.
[tex]\quad \boxed{(a +b)^2 = a^2 +2ab +b^2 \, ; \, \forall \, a, \, b \, \in \mathbb{R}}[/tex].
Para conhecer outras identidades algébricas que vocês podem utilizar na resolução de vários problemas, cliquem AQUI.
Solução 1
Seja [tex]X=(10^{4n^2+8}+1)^2[/tex].
Utilizando o “quadrado da soma”, temos que:
[tex]\begin{align*}X=(10^{4n^2+8}+1)^2& =(10^{4n^2+8})^2+2\cdot (10^{4n^2+8})+1^2\\
&=10^{8n^2+16}+2\cdot10^{4n^2+8}+1\\
&=1\underbrace{000\,\,\,\,\cdots\,\,\,\,000}_{8n^2+16\,\text{algarismos}\,0}+2\underbrace{000\,\,\,\,\cdots\,\,\,\,000}_{4n^2+8\,\text{algarismos}\,0}+1\\
&=1\,\,\underbrace{000\,\,\,\,\cdots\,\,\,\,000}_{4n^2+7\,\text{algarismos}\,0}\,\,2\,\,\underbrace{000\,\,\,\,\cdots\,\,\,\,000}_{4n^2+8\,\text{algarismos}\,0}+1 \\
&=1\,\,\underbrace{000\,\,\,\,\cdots\,\,\,\,000}_{4n^2+7\,\text{algarismos}\,0}\,\,2\,\,\underbrace{000\,\,\,\,\cdots\,\,\,\,000}_{4n^2+7\,\text{algarismos}\,0}1 \, .\end{align*}[/tex]
Veja o esqueminha:
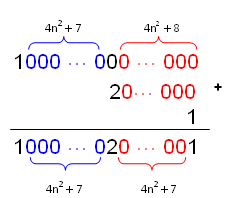
Portanto, a soma dos dígitos do número [tex]X[/tex] é sempre [tex]\fcolorbox{black}{#FFC0CB}{$1+2+1=4$}[/tex] e, assim, independe do inteiro positivo [tex]n[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
Considerando [tex]4n^2 + 8 = x[/tex], temos que:
- [tex](10^x + 1)^2 = (10^x)^2 + 2(10^x\cdot1) + 1^2 = 10^{x\cdot2} + 2\cdot{10^x} + 1[/tex].
Veja que os primeiros algarismos desse número (da esquerda para a direita) serão o [tex]1[/tex] seguido de [tex]x – 1[/tex] zeros. Após isso, teremos o algarismo [tex]2[/tex] seguido de [tex]x – 1[/tex] zeros e, por fim, o algarismo [tex]1[/tex] como unidade.
Assim, podemos ver que a soma dos dígitos deste número é igual a [tex]\boxed{1 + 2 + 1 = 4}[/tex] e que [tex]n[/tex] não influencia este resultado.
Solução elaborada pelo Clube 1uik, com contribuições dos Moderadores do Blog.