Problema
(Indicado a partir do 1º ano do E. M.)
Sejam as funções [tex]f:\mathbb{R}\rightarrow\mathbb{R}[/tex] e [tex]g:\mathbb{R}\rightarrow\mathbb{R}[/tex] definidas por [tex]f(x)=x^2+ax[/tex] e [tex]g(x)=-x^2+bx,[/tex] em que [tex]a, b \in\mathbb{R}[/tex].
Considere que [tex]f[/tex] e [tex]g[/tex] satisfazem as seguintes condições:

Determine a soma de todos os valores de [tex]x[/tex] para os quais [tex]f\circ g(x)=0[/tex].

Lembretes
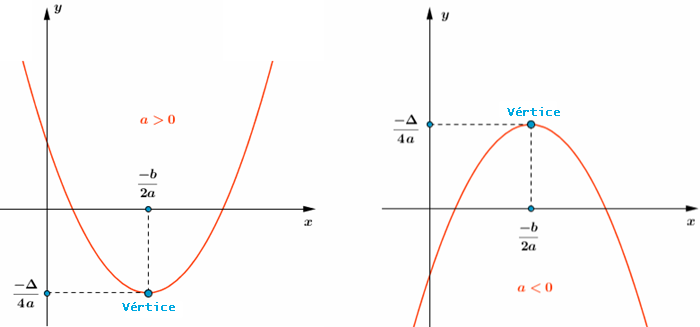
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a} \, [/tex] e [tex] \, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução
Primeiramente, observem que no enunciado da questão o [tex]a[/tex] e o [tex]b[/tex] não estão em seus papéis tradicionais (o [tex]a[/tex] sendo o coeficiente do termo [tex]x^2[/tex] e o [tex]b[/tex] o coeficiente do [tex]x[/tex]) na expressão geral [tex]\boxed{ax^2+bx+c}[/tex] que aparece nas fórmulas envolvendo funções quadráticas ou equações do segundo grau. Mas, mesmo assim, percebe-se que os gráficos de [tex]f[/tex] e de [tex]g[/tex] são parábolas com concavidades voltadas para cima e para baixo, respectivamente. Portanto, podemos utilizar o lembrete [tex]{\color{#800000}(2)}[/tex] para obtermos as regras que definem [tex]f[/tex] e [tex]g[/tex], calcularmos [tex]f\circ g(x)[/tex] e finalizarmos o problema. Vamos lá!
- Analisando as informações sobre a função [tex]f[/tex] e utilizando o lembrete [tex]{\color{#800000}(2)}[/tex], temos [tex]y_v=\frac{-a^2}{4}=-4[/tex].
Dessa forma, [tex]-a^2=-16[/tex], ou seja, [tex]a=\pm 4[/tex].
A tabelinha dada no problema informa que o ponto de mínimo é negativo, então [tex]x_v=\dfrac{-a}{2}<0[/tex], donde [tex]a>0[/tex]. Assim, [tex]a=4[/tex] e podemos então concluir que [tex]\boxed{f(x)=x^2+4x}[/tex]. - Da mesma forma, vamos analisar os dados que temos sobre a função [tex]g[/tex].
Perceba que agora [tex]y_v=\frac{-b^2}{-4}=\frac{25}{4}[/tex], logo [tex]b=\pm 5[/tex].
Como o ponto de máximo é positivo, então [tex]x_v=\dfrac{-b}{-2}\gt0[/tex], donde [tex]b\gt0[/tex] e daí podemos concluir que [tex]b=5[/tex] e, portanto, [tex]\boxed{g(x)=-x^2+5x}[/tex]. - Fazendo a composição [tex]f\circ g(x)[/tex], encontramos:
[tex]\qquad \boxed{f\circ g(x)=(-x^2+5x)^2+4(-x^2+5x)}[/tex], [tex] \qquad \textcolor{#800000}{(i)}[/tex]
ou ainda,
[tex]\qquad \boxed{f\circ g(x)=x^4-10x^3+21x^2+20x}.[/tex]
Agora vamos determinar os valores [tex]x[/tex] tais que [tex]f\circ g(x)=0[/tex].
Utilizando a igualdade [tex]\textcolor{#800000}{(i)}[/tex], temos que:
[tex]\qquad \begin{align*} f\circ g(x)&=(−x^2+5x)^2+4(−x^2+5x)\\
&=(−x^2+5x)\left[(−x^2+5x)+4\right]\\
&=x\left(-x+5\right)\left(-x^2+5x+4\right).\end{align*}[/tex]
Dessa forma:
[tex]\qquad f\circ g(x)=0 \iff x(-x+5)(-x^2+5x+4)=0[/tex]
[tex] \quad \quad \qquad \qquad \iff \, \boxed{x=0} [/tex] ou [tex] \, \boxed{-x+5=0} [/tex] ou [tex] \, \boxed{-x^2+5x+4=0}[/tex].
Logo, resolvendo as três equações acima, determinamos todos os valores de [tex]x[/tex] para os quais [tex]f\circ g(x)=0[/tex]:
[tex]\qquad \qquad 0[/tex], [tex]5[/tex], [tex]\dfrac{5-\sqrt{41}}{2} \, [/tex] e [tex]\dfrac{5+\sqrt{41}}{2}[/tex].
Portanto, a soma pedida é [tex]\fcolorbox{black}{#eee0e5}{$S=0+5+\dfrac{5-\sqrt{41}}{2} + \dfrac{5+\sqrt{41}}{2}= 10$}[/tex].
Observamos que é possível obtermos os valores de [tex]x[/tex] para os quais [tex]f\circ g(x)=0[/tex] sem sequer calcularmos a expressão final de [tex]f\circ g(x)[/tex] como fizemos acima.
Basta utilizarmos apenas as igualdades [tex]\boxed{f(x)=x^2+4x}[/tex] e [tex]\boxed{g(x)=-x^2+5x}[/tex].
Observe, inicialmente, que:
[tex]\qquad f(x)=0\iff x^2+4x=0 \iff x\cdot(x+4)=0 \iff x=0 \textrm{ ou } x=-4[/tex].
Assim, em particular,
[tex]\qquad f\circ g(x)=0\iff f\left(g(x)\right)=0\iff g(x)=0 \textrm{ ou }g(x)=-4[/tex].
Mas:
[tex]\quad (a) \, g(x)=0 \iff -x^2+5x=0 \iff x\cdot (-x+5)=0 \iff x=0 \textrm{ ou } x=5[/tex];
[tex]\quad \begin{align*} (b) \, g(x)=-4 & \iff -x^2+5x=-4 \iff -x^2+5x+4=0 \\
& \iff x=\dfrac{-5\pm\sqrt{5^2-4\cdot(-1)\cdot4}}{2\cdot(-1)} \\
& \iff x=\dfrac{5-\sqrt{41}}{2} \textrm{ ou } \dfrac{5+\sqrt{41}}{2}; \end{align*} [/tex]
logo, a soma [tex]S[/tex] de todos os valores de [tex]x[/tex] para os quais [tex]f\circ g(x)=0[/tex] é dada por [tex] \fcolorbox{black}{#eee0e5}{$S=0+5+\dfrac{5-\sqrt{41}}{2} + \dfrac{5+\sqrt{41}}{2}= 10$}[/tex] .
Soluções elaboradas pelos Moderadores do Blog.