.Problema: Relógio Digital

Problema
(Indicado a partir do 2º ano do E. M.)

Um relógio digital mostra, utilizando quatro dígitos, todas as horas possíveis de 00:00 a 23:59. Os dígitos do relógio são como os da figura abaixo.

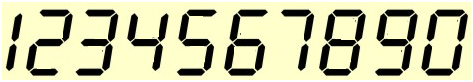
De frente para o relógio se coloca um espelho. Determinar a quantidade de vezes em um dia nas quais a imagem do relógio mostra algum horário possível.

Solução 1

Observe, inicialmente, que:

(i) Quando os algarismos [tex]0, 1, 2, 5, 8[/tex] são refletidos, eles geram os algarismos [tex]0, 1, 5, 2, 8[/tex], respectivamente.
Os demais dígitos não geram nenhum outro dígito dentre os possíveis.

(ii) Os dígitos das dezenas nas horas e nos minutos, na imagem refletida, correspondem aos dígitos das unidades nos minutos e nas horas, respectivamente.

(iii) Como em nenhum momento temos o [tex]8[/tex] nas dezenas das horas e dos minutos, descartamos o [tex]8[/tex] e ficamos apenas com os dígitos [tex]0, 1, 2, 5[/tex].

Perceba agora que, com os dígitos [tex]0, 1, 2, 5[/tex], podemos formar [tex]11[/tex] horas distintas:

[tex]00, 01, 02, 05, 10, 11, 12, 15, 20, 21, 22[/tex],

e todas elas refletidas geram respectivamente minutos possíveis:

[tex]00, 10, 50, 20, 01, 11, 51, 21, 05, 15, 55[/tex].

Também podemos perceber que os valores dos minutos que após refletidos geram possíveis horas são exatamente os já descritos. Então, para cada um dos [tex]11[/tex] valores das horas que geram possíveis minutos, há [tex]11[/tex] possíveis minutos que geram possíveis horas.
Portanto, teremos em um dia um total de [tex]11\times 11=121[/tex] vezes nas quais a imagem refletida corresponderá a uma possível hora.

Solução elaborada pelos Moderadores do Blog.

Solução 2

Primeiramente, notamos que os únicos algarismos que ao terem sua imagem refletida permanecem algarismos são [tex]0[/tex],[tex]1[/tex], [tex]2[/tex], [tex]5[/tex] e [tex]8[/tex], sendo que ao serem refletidos [tex]2[/tex] torna-se [tex]5[/tex] e vice-versa.
Veja que o [tex]8[/tex] mesmo no relógio normal só poderia ocupar a segunda casa das horas formando as [tex]08[/tex] ou [tex]18[/tex] horas ou a segunda casa dos minutos formando [tex]08[/tex], [tex]18[/tex], [tex]28[/tex], [tex]38[/tex], [tex]48[/tex] e [tex]58[/tex] minutos. Porém, notamos que horários formados com o número [tex]8[/tex] ao serem espelhados mostram horários impossíveis. Visualize a afirmação clicando no botão abaixo.

Logo, todos os horários que continuam possíveis ao serem espelhados são formados pelos algarismos [tex]0[/tex], [tex]1[/tex], [tex]2[/tex] e [tex]5[/tex].
A seguir, analisamos os horários possíveis no relógio utilizando os algarismos [tex]0[/tex], [tex]1[/tex], [tex]2[/tex] e [tex]5[/tex] para assim inverter e ver quais horários continuariam possíveis no espelho.
No relógio temos as seguintes possibilidades:

Hora

Na primeira casa das horas temos três opções: [tex]0[/tex], [tex]1[/tex] ou [tex]2[/tex]. Mas repare que os algarismos [tex]0[/tex] e [tex]1[/tex] podem ir com o algarismo [tex]5[/tex], mas o [tex]2[/tex] não. Assim, vamos dividir em dois casos.

Caso [tex]1[/tex]
Primeira casa: [tex]0[/tex] ou [tex]1[/tex]
Segunda casa: [tex]0[/tex], [tex]1[/tex], [tex]2[/tex] ou [tex]5[/tex]
Caso [tex]2[/tex]
Primeira casa: [tex]2[/tex]
Segunda casa: [tex]0[/tex], [tex]1[/tex] ou [tex]2[/tex]

Minutos

Para os minutos temos as seguintes possibilidades:

Primeira casa: [tex]0[/tex], [tex]1[/tex], [tex]2[/tex] ou [tex]5[/tex]
Segunda casa: [tex]0[/tex], [tex]1[/tex], [tex]2[/tex] ou [tex]5[/tex]

Agora basta inverter e contar as possibilidades no espelho. Para isso devemos primeiramente entender que se no relógio o horário é [tex]wx:yz[/tex], no espelho será [tex]zy:xw[/tex].
Vamos lá.

Hora

Os minutos no relógio são as horas no espelho, sendo que se os minutos são [tex]yz[/tex] no relógio, as horas se tornam [tex]zy[/tex] no espelho. Veja que assim como fizemos anteriormente, será necessário dividir em dois casos pois não existe [tex]25:00[/tex]:

Caso [tex]EH.1[/tex]

Assim para o primeiro caso das horas há [tex]2 \times 4 = 8[/tex] possibilidades.

Caso [tex]EH.2[/tex]

Assim, para o segundo caso das horas há [tex]1 \times 3 = 3[/tex] possibilidades.

Devemos escolher o caso [tex]EH.1[/tex] ou o caso [tex]EH.2[/tex]. Logo, há [tex]8 + 3 = 11[/tex] possibilidades das horas aparecerem no espelho.

Minutos

Os minutos no espelho foram as horas no relógio, sendo que se as horas no relógio eram [tex]wx[/tex] os minutos no espelho se tornam [tex]xw[/tex]. Como as horas estavam divididas em casos, vamos inverter e analisá-los individualmente:

Caso [tex]EM.1[/tex]

Assim para o primeiro caso há [tex]4 \times 2 = 8[/tex] possibilidades.

Caso [tex]EM.2[/tex]

Como podemos ver para o segundo caso há [tex]3[/tex] possibilidades.

Pode haver no espelho o caso [tex]EM.1[/tex] ou o caso [tex]EM.2[/tex]. Assim há [tex]8 + 3 = 11[/tex] possibilidades para os minutos.

Se há [tex]11[/tex] possibilidades para as horas e [tex]11[/tex] possibilidades para os minutos então temos que há [tex]11 × 11 = 11^2 = 121[/tex] horários possíveis no espelho.
Em suma, a quantidade de vezes em um dia nas quais a imagem do relógio mostra algum horário possível é [tex]121[/tex].

Solução elaborada pelo Clube 1uik, com contribuições dos Moderadores do Blog.

Participou da discussão o Clube: 1uik.