Problema
(Indicado a partir do 9º ano do E. F.)
Por um ponto [tex]P[/tex] no interior de um retângulo [tex]ABCD[/tex], traçamos retas paralelas aos lados desse retângulo, de modo que o dividimos em quatro retângulos menores (cada um deles com vértice em [tex]P[/tex]).
Sejam [tex]S_1[/tex], [tex]S_2[/tex] e [tex]S_3[/tex] as áreas dos retângulos menores que têm vértices em [tex]D[/tex], em [tex]A[/tex] e em [tex]B[/tex], respectivamente. Determine a área do quarto retângulo menor em função de [tex]S_1[/tex], [tex]S_2[/tex] e [tex]S_3[/tex].
Solução
Considere a figura abaixo, que ilustra a geometria do problema proposto.
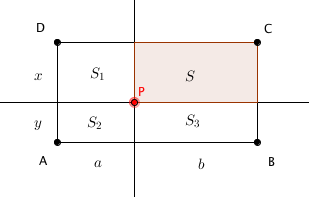
Com base nas medidas indicadas na figura, temos que a área [tex]S[/tex] procurada é
[tex]\qquad \begin{align}S &= b \cdot x \\
&= (b\cdot 1) \cdot (x\cdot 1)
\\ &= \bigg(b\cdot \dfrac{y}{y}\bigg)\cdot \bigg(x\cdot \dfrac{a}{a}\bigg)
\\&= \dfrac{by}{y} \cdot \dfrac{ax}{a} \\
&= \dfrac{by \cdot ax}{ay} = \fbox{$\dfrac{S_3 \cdot S_1}{S_2}$}.\end{align}[/tex]
Solução elaborada pelos Moderadores do Blog.
