Problema
(Indicado a partir do 9º ano do E. F.)
(a) Prove que um quadrado pode ser dividido em 2016 quadrados.
(b) Um quadrado pode ser dividido em 2017 quadrados?
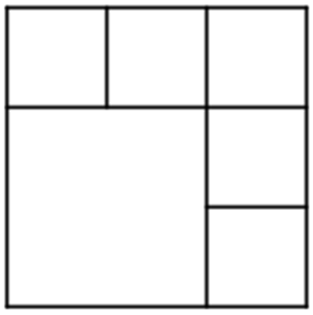
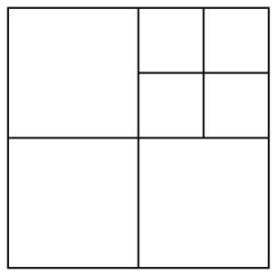
Por exemplo, a figura abaixo mostra um quadrado dividido em 7 quadrados.
Solução 1
De fato, basta dividir um quadrado qualquer em quatro iguais: a nova configuração ganha quatro quadrados menores e perde um dos quadrados iniciais.
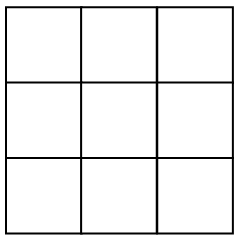
Assim, dividindo um quadrado em [tex]9[/tex] quadrados,
podemos obter configurações com [tex]12, 15, 18[/tex] quadrados
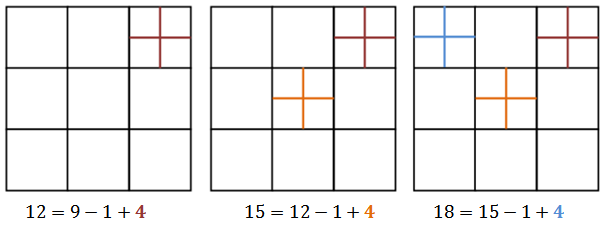
e todos os múltiplos de [tex]3[/tex] subsequentes, incluindo [tex]2016[/tex].
Para [tex]2017[/tex] a solução é idêntica, bastando alterar a configuração inicial. Começando com quatro quadrados,
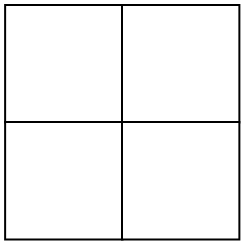
obtemos configurações para [tex]7,10, 13[/tex], …,
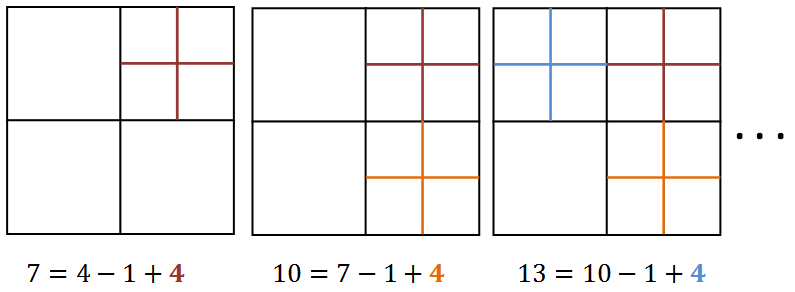
isto é, todos os números que deixam resto [tex]1[/tex] ao serem divididos por [tex]3[/tex], incluindo [tex]2017[/tex].
Na verdade, pode-se dividir um quadrado em qualquer número de quadrados maior do que cinco. Veja:
|
|
A partir desta divisão de um quadrado qualquer em seis quadrados internos, podemos obter a divisão do quadrado inicial em [tex]3n[/tex] quadrados internos, para qualquer número natural [tex]n[/tex] maior do que [tex]1[/tex] ( [tex]\forall n \in \mathbb{N}, \, n \gt 1[/tex]). |
|
|
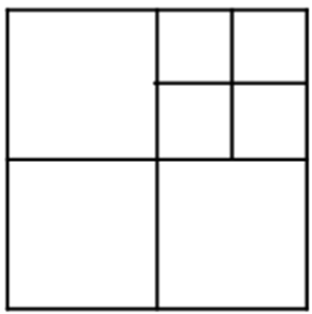
A partir desta divisão de um quadrado qualquer em sete quadrados internos, podemos obter a divisão do quadrado inicial em [tex]3n+1[/tex] quadrados internos, para qualquer número natural [tex]n[/tex] maior do que [tex]1[/tex] ( [tex]\forall n \in \mathbb{N}, \, n \gt 1[/tex]). |
|
|
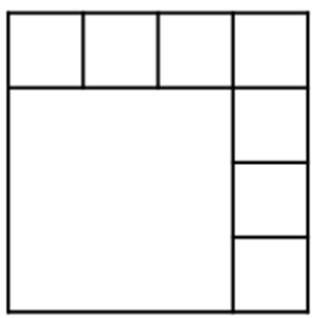
A partir desta divisão de um quadrado qualquer em oito quadrados internos, podemos obter a divisão do quadrado inicial em [tex]3n+2[/tex] quadrados internos, para qualquer número natural [tex]n[/tex] maior do que [tex]1[/tex] ( [tex]\forall n \in \mathbb{N}, \, n \gt 1[/tex]). |
Solução elaborada pelos Moderadores do Blog.
Solução 2
Observe que podemos dividir um quadrado em no mínimo [tex]4[/tex] quadrados. A partir daí, podemos dividir um dos quadrados menores em outros quatro quadrados, desse modo teremos [tex]4 + 3[/tex] quadrados, isso porque adicionamos quatro quadrados, mas subtraímos um. Podemos fazer isso com outro quadrado, obtendo [tex]4 + 6[/tex] quadrados, com outro quadrado obtendo [tex]4 + 9[/tex] quadrados, com outro quadrado obtendo [tex]4 + 12[/tex] quadrados etc.
Desse modo, é possível concluir que um quadrado pode ser dividido em [tex]4 + 3n[/tex] quadrados, [tex]n[/tex] natural. De acordo com isso, podemos dividir um quadrado em [tex]2017[/tex] quadrados.
Agora, em vez de começar dividindo um quadrado em outros [tex]4[/tex] quadrados, nós podemos começar dividindo em [tex]9[/tex] quadrados. A partir daí basta dividir os quadrados menores em [tex]4[/tex]. Neste caso nós podemos dividir um quadrado em [tex]9 + 3x[/tex] quadrados, [tex]x[/tex] natural, o que é exatamente [tex]2016[/tex]:
[tex]\qquad 2016 = 9 + 3x[/tex]
[tex]\qquad 2016 – 9 = 3x[/tex]
[tex]\qquad 2007 = 3x[/tex]
[tex]\qquad\dfrac{2007}{3} = x[/tex]
[tex]\qquad 669 = x[/tex]
Com isso provamos o item (a) e respondemos positivamente o item (b).
Solução elaborada pelo COM 1uik, com contribuições dos Moderadores do Blog.
Aprofundando a discussão . . .
Podemos observar que no enunciado do problema não existe a restrição de que os quadrados resultantes da divisão tenham medidas diferentes entre si.
Perceba que, com essa restrição, as divisões em [tex]9, 12, 15, 18[/tex] quadrados que fizemos não estariam corretas,
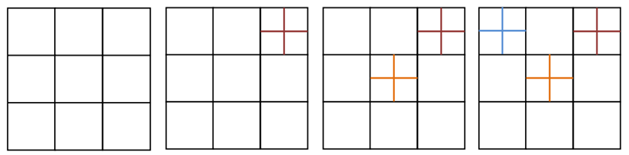
assim como as divisões feitas em [tex]4, 7,10, 13[/tex] quadrados.
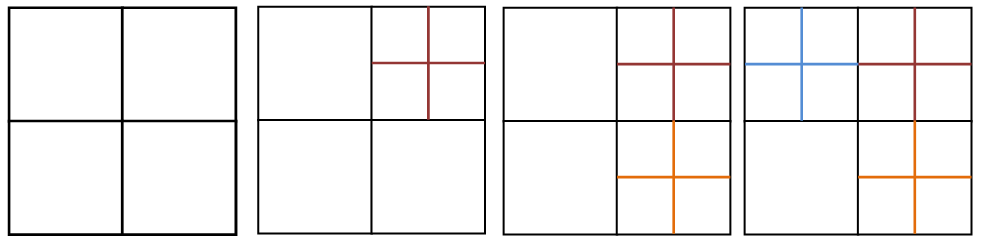
Observe que a argumentação de que “uma configuração qualquer na qual um quadrado está dividido em [tex]N[/tex] quadrados pode ser alterada de modo que a nova configuração tenha [tex]N+3[/tex] quadrados” não será correta se exigirmos quadrados com medidas diferentes: ao dividirmos um dos quadrados iniciais com tamanhos diferentes em quatro outros quadrados, estes quatro terão lados com o mesmo comprimento.
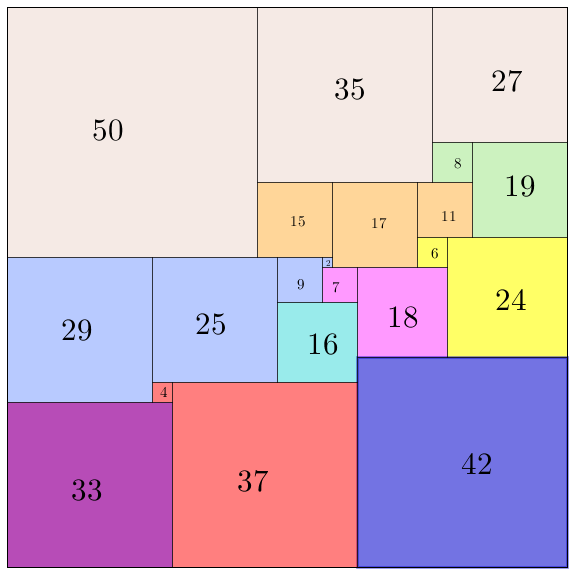
O problema de se dividir um quadrado em quadrados menores, todos com tamanhos distintos, é chamado de dissecção perfeita de um quadrado e é algo não trivial de se fazer. Nesse tipo de problema, é usual se trabalhar com quadrados cujos comprimentos dos lados são números inteiros positivos.
Isso seria como montar um quadrado com [tex]21[/tex] quadrados menores, todos com lados de medidas inteiras e distintas!
Clique no próximo botão e veja um gif animado da solução.
Se você se interessou pelo assunto, clique no próximo botão!