.Problema para ajudar na escola: Latas de tinta

Problema
(A partir da 2ª série do E. M.) (Nível: Médio)

---

(Adaptado do ENEM 2014) Uma lata de tinta, com a forma de um paralelepípedo retangular reto, tem as bases quadradas, conforme mostra a figura abaixo.

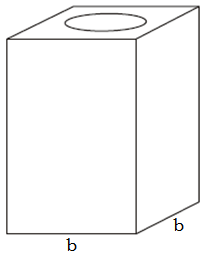
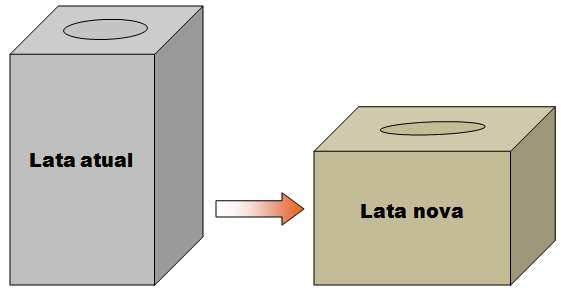
Será produzida uma nova lata com o mesmo formato, mas com as dimensões da base [tex]25\%[/tex] maiores do que as da lata atual.
O que deve acontecer com a dimensão da altura da nova lata para que esta comporte a mesma quantidade de tinta da lata atual?

Solução 1

---

Sabemos que o formato das latas novas será o mesmo das latas atuais: um paralelepípedo retangular reto com bases quadradas. Assim, se denotarmos por:

• [tex]b[/tex] a medida de cada lado das bases da lata atual;
• [tex]b_n[/tex] a medida de cada lado das bases da nova lata;
• [tex]h[/tex] a altura da lata atual;
• [tex]h_n[/tex] a altura da nova lata;
• [tex]V[/tex] o volume da lata atual;
• [tex]V_n[/tex] o volume da nova lata;

teremos que [tex]\boxed{V=b^2 \cdot h}[/tex] e [tex]\boxed{V_n=b_n^2 \cdot h_n}[/tex].
As dimensões da base da nova lata serão [tex]25\%[/tex] ([tex]\frac{25}{100}[/tex]) maiores do que as dimensões da base da lata atual, então:
[tex]\qquad b_n=b+\dfrac{25}{100}b=b+\dfrac{1}{4}b=\dfrac{5}{4}b.[/tex]
Mas a nova lata deverá comportar a mesma quantidade de tinta da lata atual; logo, os volumes das duas latas são iguais e, assim,
[tex]\qquad b^2 \cdot h=b_n^2 \cdot h_n[/tex].

Como [tex] b_n=\dfrac{5}{4}b[/tex], segue que

[tex]\qquad b^2 \cdot h=\left(\dfrac{5}{4}b \right)^2 \cdot h_n[/tex],
ou seja,
[tex]\qquad h=\dfrac{25}{16} h_n[/tex],
ou ainda,
[tex]\qquad h_n=\dfrac{16}{25} h[/tex].

Perceba que [tex]\dfrac{16}{25}= \dfrac{64}{100}[/tex], portanto,

[tex]\qquad h_n=\dfrac{64}{100} h[/tex].

Dessa forma, podemos concluir que a nova lata deverá ter uma altura correspondente a [tex]64\%[/tex] da altura da lata atual. Isso significa que a medida da altura atual terá uma redução de [tex]36\%[/tex].

---

Solução elaborada pelos Moderadores do Blog.

Solução 2

---

Sabe-se que o volume de um prisma retangular é calculado da seguinte maneira: (área da base) x (altura) .
Com o aumento das dimensões da base, a área da base passa a ser [tex]\dfrac{25}{16}\cdot b^2[/tex]; assim, a fim de que o volume não se altere, deve-se multiplicar a altura da lata atual por[tex]\dfrac{ \, \, \, 1 \, \, \, }{\frac{25}{16}}=\dfrac{16}{25}=0,64[/tex].
Assim, a nova lata tem uma altura cuja dimensão representa [tex]64\%[/tex] da altura da lata atual.

---

Solução elaborada pelo COM Paralelo 38.