✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F.) (Nível: Médio)
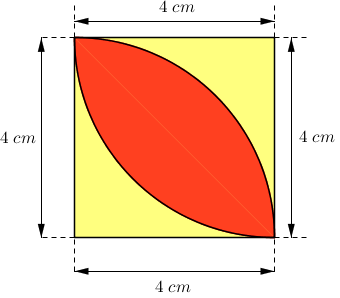
Na figura, os arcos são quadrantes centrados em vértices do quadrado.
Qual a área da região colorida de vermelho?
Solução 1
Observe a figura abaixo.
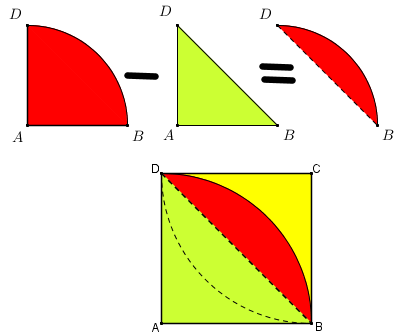
Perceba que, se da área do quadrante [tex]ABD[/tex] retirarmos a área interna ao triângulo [tex]ABD[/tex], obtemos metade da área da pétala, ou seja, metade da área da região vermelha solicitada no problema.
Então, vamos lá:
- área do círculo de centro em [tex]A[/tex] e raio [tex]4[/tex]: [tex]A_c= \pi \times 4^2=16 \pi \, cm^2[/tex];
- área do quadrante [tex]ABD[/tex]: [tex]A_Q=\dfrac{A_c}{4}=4\pi \, cm^2[/tex];
- área do triângulo [tex]ABD[/tex]: [tex]A_t= \dfrac{4\times 4}{2}=8 \, cm^2[/tex];
assim, a metade da área da pétala é
[tex]\qquad A_Q – A_t=4\pi-8 \, cm^2[/tex]
e, portanto, a área da região colorida de vermelho é
[tex]\qquad A_v=2 \times \left(A_Q – A_t\right)=2\times \left(4\pi-8 \right) \, cm^2[/tex].
Podemos obter uma aproximação para esse valor, considerando para [tex]\pi[/tex] um valor aproximado de [tex]3,14[/tex]:
[tex]\qquad A_v=2\times \left(4\pi-8 \right)=8\pi-16 \approx 8 \times 3,14-16=9,12 \, cm^2[/tex].
Dessa forma, a área da região colorida de vermelho é, aproximadamente, [tex]\boxed{9,12 \, cm^2}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
Observe a próxima figura.
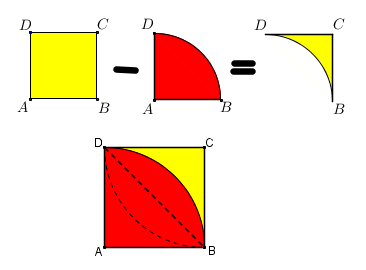
Note que, se retirarmos a área do quadrante [tex]ABD[/tex] da área interna do quadrado [tex]ABCD[/tex], obtemos metade da área a ser retirada do quadrado [tex]ABCD[/tex] para obtermos a pétala.
A área do quadrado [tex]ABCD[/tex] é de [tex]16 \, cm^2[/tex] e a área do quadrante já vimos que é [tex]4\pi \, cm^2[/tex], então a área da pétala é
[tex]\qquad 16-2 \times (16- 4 \pi)= \left(8 \pi-16 \right) \, cm^2[/tex],
o que também já sabemos ser aproximadamente [tex]\boxed{9,12 \, cm^2}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 3
A área da pétala é [tex]9, 12\, cm^2[/tex].
Para encontrarmos este valor, primeiro calculamos a área do círculo cujo centro é o vértice à esquerda de baixo do quadrado em que se encontra a figura da pétala. Seu raio será [tex]4\, cm[/tex], então elevamos esse valor ao quadrado, e multiplicamos por [tex]\pi[/tex] (aproximadamente [tex]3, 14[/tex]), encontrando [tex]50, 24\, cm^2[/tex].
Depois, dividimos por [tex]4[/tex] para obtermos a área de um quadrante, [tex]12,56\, cm^2[/tex]. Daí, para descobrirmos a área da pétala, retiramos da área do quadrante a área de um triângulo retângulo, a metade do quadrado em que se localiza a pétala, que é [tex]8\, cm^2[/tex], pois a base do triângulo é [tex]4[/tex] e sua altura também é [tex]4[/tex], ou seja, sua área é [tex]\dfrac{4\times4}{2}=8\,cm^2[/tex].
Subtraindo esse valor da área do quadrante, dará [tex]4,56\, cm^2[/tex], que é metade da área da pétala. Portanto, multiplicamos este valor por [tex]2[/tex] e temos a área da pétala, [tex]\boxed{9, 12\, cm^2}[/tex].
Solução elaborada pelo COM Os Aritméticos, com contribuições dos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
