Problema
(Indicado a partir do 9º ano do E. F.)
No edifício mais alto de Terra Brasilis moram Eduardo e Augusto.
O número do andar do apartamento de Eduardo coincide com o número do apartamento de Augusto.
A soma dos números dos apartamentos dos dois é 2164.
Calcule o número do apartamento de Eduardo sabendo que há 12 apartamentos por andar.
(Por exemplo, no primeiro andar estão os apartamentos de 1 a 12, no segundo, de 13 a 24, e assim por diante).
Solução 1
Seja [tex]a[/tex] o andar do apartamento de Eduardo. Então, o número de seu apartamento é [tex]n=12(a – 1) + b,[/tex] com [tex]1 \leqslant b \leqslant 12.[/tex]
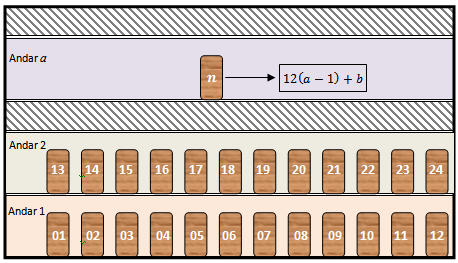
Já que [tex]a[/tex] é o andar do apartamento de Eduardo, então é também o número do apartamento de Augusto. Assim, [tex]a+n=2164[/tex], ou seja, [tex] a + 12(a – 1) + b = 2164[/tex], donde, [tex] \boxed{b= 2176 – 13a}[/tex].
Mas, [tex]1 \leqslant b \leqslant 12[/tex], logo:
[tex]\qquad 1 \leqslant 2176 – 13a \leqslant 12\\
\qquad 0\lt2176-13a\lt13\\
\qquad 13a\lt 2176\lt 13a+13\\
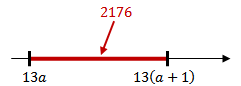
\qquad 13a\lt 2176\lt 13(a+1),[/tex]
e, assim, [tex]2176[/tex] está entre dois múltiplos consecutivos de [tex]13.[/tex]
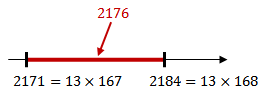
Observe que
|
|
||||
| donde [tex]2176=13\times 167+5[/tex]. Com isso, [tex]2176[/tex] está entre [tex]13\times 167[/tex] e [tex]13\times 168.[/tex] |
Dessa forma, [tex]a=167[/tex], [tex]b=2176-13\times 167=5[/tex] e, portanto, o número do apartamento de Eduardo é:
[tex]\qquad12(a – 1) + b = 12 \times 166 + 5 = \boxed{1997}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Seja [tex]n[/tex] o número do andar do apartamento de Eduardo. Logo, o número do apartamento de Augusto é, também, [tex]n[/tex].
Como a soma dos números dos apartamentos é [tex]2164[/tex], o número do apartamento de Eduardo é [tex]2164 – n[/tex].
Sabe-se que no [tex]n[/tex]-ésimo andar estão os apartamentos de números [tex]12(n-1)+1[/tex] a [tex]12n[/tex]; assim, o número do apartamento de Eduardo deve obedecer à seguinte desigualdade:
[tex]\qquad 12(n-1)+1 \leq 2164 – n\leq 12n[/tex].
Resolvendo a primeira parte:
[tex]\qquad 12(n-1)+1 \leq 2164 – n[/tex]
[tex]\qquad 12n-11 \leq 2164 – n[/tex]
[tex]\qquad 13n \leq 2175[/tex]
Resolvendo a segunda parte:
[tex]\qquad 2164 – n \leq 12n[/tex]
[tex]\qquad 2164 \leq 13n[/tex]
Logo [tex]2164 \leq13 n \leq 2175[/tex].
Dividindo toda a desigualdade por [tex]13[/tex], vemos que o único valor inteiro que [tex]n[/tex] pode assumir é [tex]n=167[/tex].
Portanto, se quisermos encontrar Eduardo basta irmos ao andar [tex]167[/tex], apartamento número [tex]1997(=2164 – 167)[/tex].
Solução elaborada pelo Clube Paralelo 38, com contribuições dos Moderadores do Blog.
