Problema
(Indicado a partir do 9º ano do E. F.)
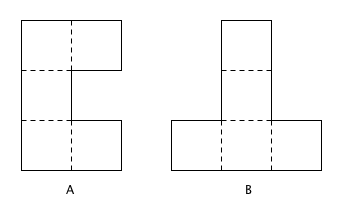
Na figura temos dois pentaminós feitos em cartolina e compostos, cada um, por cinco quadrados de lados unitários.
Recorte o pentaminó A em quatro pedaços e o pentaminó B em três pedaços; a seguir, utilize esses sete pedaços para montar uma peça quadrada.
Ferramentas que ajudam
Para resolver este problema precisaremos de uma definição e de uma propriedade.
Um triângulo retângulo é qualquer triângulo que tenha um ângulo reto, isto é, um ângulo de 90 graus.
 |
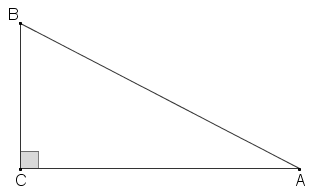Se na figura o ângulo relativo ao vértice [tex]C[/tex] for reto, então o triângulo [tex]ABC[/tex] é um triângulo retângulo. Os lados de um triângulo retângulo recebem denominações especiais. Assim, no triângulo [tex]ABC[/tex]: ● os lados [tex]\overline{CB} \, [/tex] e [tex] \, \overline{CA}[/tex] são denominados catetos; ● o lado [tex] \, \overline{AB}[/tex], oposto ao ângulo reto, é denominado hipotenusa. |
Teorema de Pitágoras – Em um triângulo, o quadrado do comprimento de um dos lados é igual à soma dos quadrados dos outros dois lados se, e somente se, o triângulo for retângulo.
Para conhecer melhor essas ferramentas, visite esta Sala.
Solução do problema
|
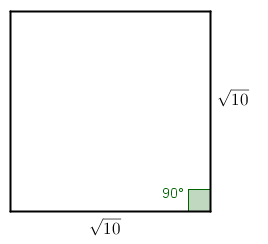
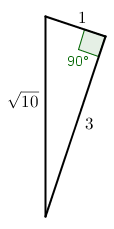
Como cada pentaminó é formado por quadrados unitários, a peça quadrada a ser montada terá área [tex]10[/tex], logo seu lado deve medir [tex]\sqrt{10}[/tex]. Podemos obter um segmento [tex]\sqrt{10}[/tex] como hipotenusa de um triângulo retângulo de catetos medindo [tex]1[/tex] e [tex]3[/tex], pois [tex](\sqrt{10})^2 = 3^2 + 1^2[/tex]. |
 |
 |
Assim, a partir dos pentaminós, podemos recortar quatro triângulos retângulos congruentes de catetos [tex]1[/tex] e [tex]3[/tex] que, posicionados de modo a obtermos um quadrado de lado [tex]10[/tex], deixam no interior uma região quadrada de lado [tex]2[/tex], facilmente preenchida com pedaços retangulares obtidos nas figuras.
Recorte: |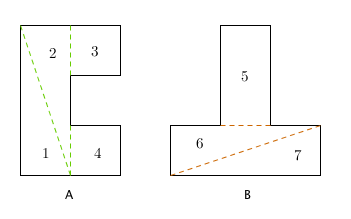
Uma montagem possível: |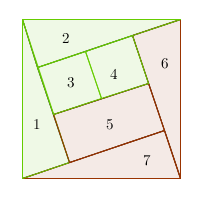
Solução elaborada pelos Moderadores do Blog.
Um aplicativo para ajudar…
Utilize este aplicativo para fazer montagens com as sete peças recortadas dos dois pentaminós de modo a formar uma peça quadrada.
Instruções:
1) Aguarde o aplicativo carregar completamente.
2) Para transladar uma das sete peças, clique sobre a peça, mantenha o mouse pressionado e arraste a peça.
3) Para rodar uma das sete peças, clique sobre o vértice da peça identificado com uma letra indexada, mantenha o mouse pressionado e rode a peça.
4) Para reiniciar a construção, clique nas setinhas que aparecem no canto superior direito do aplicativo.
OBMEP_ srdg, criado com o GeoGebra