Problema
(Indicado a partir do 8º ano do E. F.)
A idade de João é [tex]T[/tex] anos. Sua idade é a soma das idades de seus três filhos.
Há [tex]N[/tex] anos, sua idade era o dobro da soma das idades dos três filhos.
Qual a razão [tex]\dfrac{T}{N}[/tex]?
Solução 1
Pelo enunciado do problema, a idade atual de João é [tex]T[/tex] anos; vamos supor que as idades atuais de seus filhos sejam [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] anos.
Assim, há [tex]N[/tex] anos:
- a idade de João era [tex]T- N[/tex];
- a idade do filho 1 de João era [tex]a- N[/tex];
- a idade do filho 2 de João era [tex]b- N[/tex];
- a idade do filho 3 de João era [tex]c- N[/tex];
conforme mostra a imagem a seguir. Para efeito da resolução deste problema, não há necessidade de se estabelecer relações entre as idades dos três filhos.
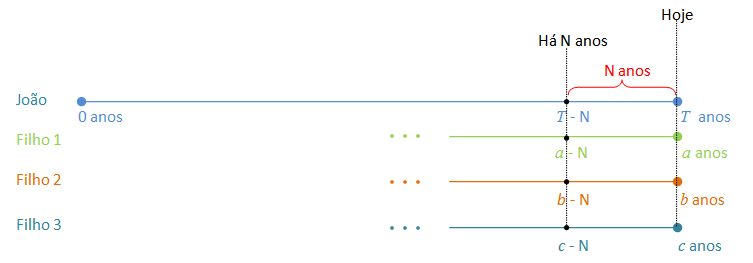
Como hoje a idade de João é a soma das idades de seus três filhos, então
[tex]\qquad T=a+b+c.\qquad \qquad (i)[/tex]
Por outro lado, há [tex]N[/tex] anos, a idade de João era o dobro da soma das idades dos seus três filhos, logo
[tex]\qquad T-N=2\left(\left(a-N \right)+\left(b-N \right)+\left(c-N \right)\right),[/tex]
donde
[tex]\qquad T=2\left(a+b+c\right)-5N.\qquad \qquad (ii)[/tex]
Assim, por [tex](i)[/tex] e [tex](ii)[/tex], temos que
[tex]\qquad T=2T-5N[/tex]
[tex]\qquad 2T-T=5N[/tex]
[tex]\qquad T=5N[/tex],
e dessa forma, [tex]\boxed{\dfrac{T}{N}=5}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
“A idade de João é [tex]T[/tex] anos. Sua idade é a soma das idades de seus três filhos.”
Considerando [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] como as idades dos três filhos, podemos concluir que:
[tex]T = a + b + c[/tex]
“Há [tex]N[/tex] anos, sua idade era o dobro da soma das idades dos três filhos. ”
Podemos representar este trecho da seguinte forma:
[tex]T – N = 2(a + b + c – 3N)[/tex]
Como [tex]T = a + b + c[/tex], também é possível representar o trecho assim:
[tex]T – N = 2(T – 3N)[/tex]
Dessa forma podemos descobrir o valor de [tex]T[/tex]:
[tex]T – N = 2(T – 3N)[/tex]
[tex]T – N = 2T – 6N[/tex]
[tex]T – 2T = -6N + N[/tex]
[tex]-T = -5N[/tex]
[tex]T = 5N[/tex]
Se[tex] \, T = 5N[/tex], logo:
[tex]\dfrac{T}{N} = \dfrac{5N}{N} = \dfrac{5\cancel{N}}{\cancel{N}} = 5[/tex]
Portanto, chegamos à conclusão de que [tex]\dfrac{T}{N}[/tex] é igual a [tex]5[/tex].
Solução elaborada pelo COM 1 uik.
