Problema
(Indicado a partir do 8º ano do E. F.)
Em uma aula de revisão sobre conjuntos numéricos às vésperas do vestibular, o professor de Jorge explicou sobre os elementos que compõem os conjuntos dos números Naturais, Inteiros, Racionais, Irracionais, Reais e Complexos.
Para dar um exemplo de determinado conjunto, o professor propôs a Jorge o seguinte problema:
“Há um número racional irredutível cujo numerador é a quantidade de moças da sala em que você estuda e o denominador é a quantidade de rapazes. A representação decimal desse número é 0,4333… Qual o número total de estudantes desta sala?”
Sabendo que Jorge acertou, qual o resultado encontrado?
Solução 1
A representação decimal [tex]0,4333…[/tex] pode ser transformada em fracionária da seguinte forma:
[tex]\qquad \qquad 0,4333\dots=\dfrac{43-4}{90}=\dfrac{39}{90}=\dfrac{13}{30}[/tex].
Portanto, nessa sala há [tex]13[/tex] moças e [tex]30[/tex] rapazes e o número total de estudantes da sala é [tex]\boxed{13+30=43}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
Para sabermos o número de moças e o número de rapazes, transformamos a dízima [tex]0, 4333…[/tex] em uma fração, como diz a dica dada no Fórum:
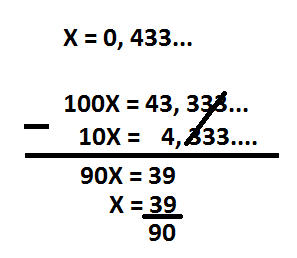Seguindo a dica, deixamos esta fração geratriz em sua forma irredutível: [tex]\dfrac{39}{90} = \dfrac{13}{30}[/tex]No enunciado diz que o numerador é a quantidade de moças e, o denominador, a quantidade de rapazes; logo, chegamos à conclusão que nesta turma existem 13 moças e 30 rapazes, ou seja, há 43 estudantes na classe.
Solução elaborada pelo COM 1uik.
Solução 3
Calculando a fração geratriz da dízima periódica [tex]0,433…[/tex], encontramos a fração [tex]\dfrac{39}{90}[/tex], que simplificando até a forma irredutível fica [tex]\dfrac{13}{30}[/tex].
Assim, o número de alunos será [tex]13+30=43[/tex].
Solução elaborada pelo COM ESQUADRÃO MATEMÁTICO, com contribuições dos Moderadores dos Clubes.
Participaram da discussão os COMs: 1uik; ESQUADRÃO MATEMÁTICO.