Problema
(Indicado a partir do 3º ano do E. M.)
Tomando o círculo máximo de um hemisfério de raio [tex]R[/tex] como base, constrói-se um cone reto de mesmo volume que o hemisfério.
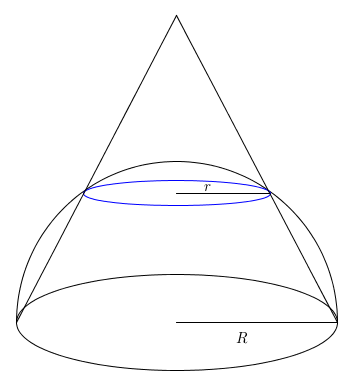
Determine o raio da circunferência produzida pela interseção da superfície lateral do cone com a superfície não plana do hemisfério, em função de [tex]R[/tex].
Solução
Sejam [tex]h[/tex] e [tex]r[/tex] a altura do cone e o raio procurado, respectivamente.
Como o volume do cone é igual ao do hemisfério, temos
[tex]\qquad \dfrac{1}{3} \cdot \pi \cdot R^2 \cdot h = \dfrac{2}{3} \cdot \pi \cdot R^3[/tex],
ou seja,
[tex]\qquad h = 2R[/tex].
Na figura abaixo, indicando a medida de [tex]D\hat{J}F[/tex] por [tex]x[/tex], perceba que
- a medida de [tex]J\hat{F}D[/tex] é [tex] 90^{\circ} – x[/tex];
- o triângulo [tex]DFH[/tex] é isósceles, logo, [tex]F\hat{H}D = 90^{\circ} – x[/tex];
- [tex]F\hat{D}H = 2x[/tex] e
- [tex]K\hat{H}D = 2x[/tex], por paralelismo.
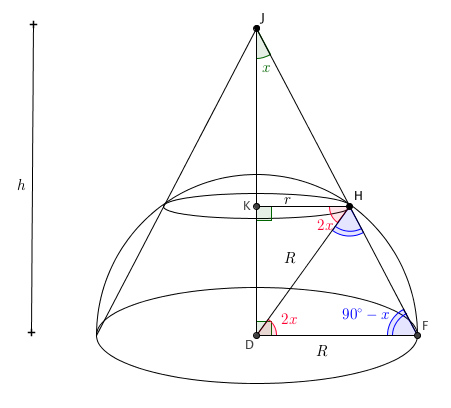
Aplicando o teorema de Pitágoras no triângulo [tex]JDF[/tex] e lembrando que [tex]h = 2R[/tex], obtemos que [tex]JF = R\sqrt{5}[/tex].
Também a partir desse triângulo, calculamos [tex]sen(x) = \dfrac{1}{\sqrt{5}} \, [/tex] e [tex] \, cos(x) = \dfrac{2}{\sqrt{5}}[/tex].
Então, da relação do cosseno do arco duplo segue que
[tex]\qquad cos(2x) = cos^2(x) – sen^2(x) = \dfrac{4}{5} – \dfrac{1}{5} = \dfrac{3}{5}[/tex].
Finalmente, observando o triângulo [tex]HDK[/tex], temos
[tex]\qquad cos(2x) = \dfrac{r}{R}[/tex]
e, assim,
[tex]\qquad \boxed{r = \dfrac{3}{5}R}[/tex].
Solução elaborada pelos Moderadores do Blog.
