Problema
(Indicado a partir do 8º ano do E. F.)
Calcule a soma das medidas dos ângulos destacados na figura.
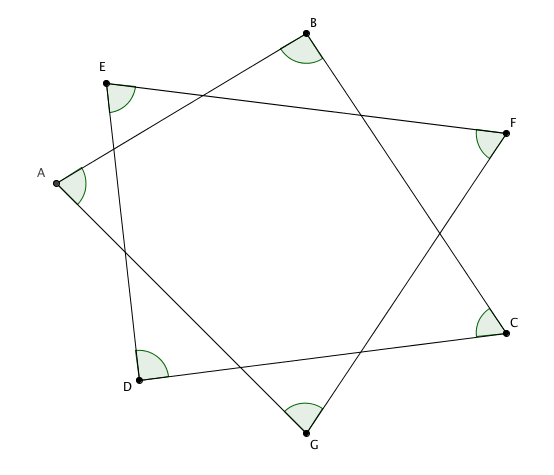
Solução 1
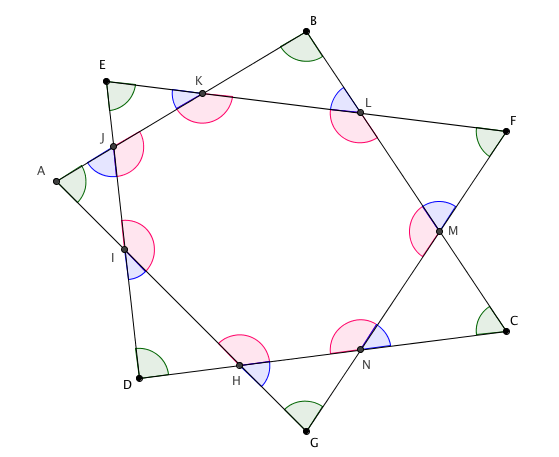
Destacamos em vermelho e azul os ângulos internos e externos do polígono HIJKLMN, respectivamente.
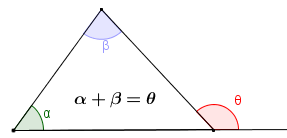Além disso, cada ângulo vermelho é a soma de um ângulo azul e verde, por ser ângulo externo de triângulo em que os ângulos internos não adjacentes são um ângulo verde e um azul. Assim, ao somarmos todos os ângulos vermelhos, acabaremos por somar todos os ângulos verdes e azuis.Indicando por [tex]S_r[/tex] a soma das medidas dos ângulos vermelhos; [tex]S_v[/tex] a soma das medidas dos ângulos verdes e [tex]S_a[/tex] a soma das medidas dos ângulos azuis, temos que [tex]\boxed{S_r = S_v + S_a} \, \, \, \, \, (i)[/tex]. Então, se queremos [tex]S_v[/tex], temos que obter [tex]S_a[/tex] e [tex]S_r[/tex], vamos lá.
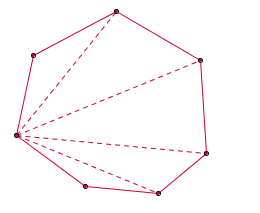Fixado um dos vértices de um heptágono convexo, como o [tex]HIJKLMN[/tex], podemos obter [tex]7-2=5[/tex] triângulos com vértices no vértice fixado e em outros dois vértices do heptágono. Observe que ao somar as medidas dos ângulos internos de cada um desses cinco triângulos obtemos a soma dos ângulos internos do heptágono inicial. Assim, lembrando que a soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex], temos que a soma das medidas dos ângulos internos de um heptágono é [tex]5\times 180^{\circ}[/tex], isto é, [tex]900^{\circ}[/tex].
Assim, em particular, [tex]\boxed{S_r=900^{\circ}} \, \, \, \, \, (ii)[/tex].- Observe que cada ângulo azul é suplementar de um, e somente um, dos vermelhos. Como temos sete pares de ângulos azuis e seus suplementares, então [tex]S_a+S_r=7\times 180^{\circ}[/tex].
Mas [tex]S_r=900^{\circ}[/tex], assim [tex]S_a=1260^{\circ}-900^{\circ}[/tex].
Portanto [tex]\boxed{S_a=360^{\circ}} \, \, \, \, \, (iii)[/tex].
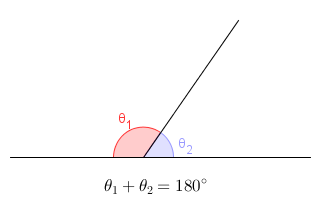
Finalizando, por[tex](i), \, (ii), \, (iii)[/tex] temos que:
[tex]\qquad S_v= S_r-S_a[/tex]
[tex]\qquad S_v= 900^{\circ}-360^{\circ}[/tex]
[tex]\qquad \boxed{S_v = 540^{\circ}}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
O heptágono [tex]HIJKLMN[/tex] da figura acima possui [tex]900^o[/tex] na soma de seus ângulos internos. Chamemos seus ângulos internos de [tex]h, i, j,k,l,m[/tex] e [tex]n[/tex], em graus.
Temos que os ângulos suplementares que pertencem aos triângulos medem respectivamente
[tex] 180^{\circ} – h, 180^{\circ}-i[/tex], no 1º triângulo;
[tex]180^{\circ}- i[/tex] e [tex]180^{\circ}-j[/tex], no 2º triângulo
e assim sucessivamente.
O ângulo verde no 1º triângulo mede [tex]180^{\circ}– (180^{\circ}- h) – (180^{\circ} – i)[/tex], o que resulta em [tex]h + i – 180^{\circ}[/tex], então, os ângulos verdes medem
[tex]h+i-180^{\circ}[/tex]
[tex]i+j-180^{\circ}[/tex]
[tex]j+k-180^{\circ}[/tex]
[tex]k+l-180^{\circ}[/tex]
[tex]l+m-180^{\circ}[/tex]
[tex]m+n-180^{\circ}[/tex]
[tex]n+h-180^{\circ}[/tex]
ou seja, sua soma é:
[tex]2h+2i+2j+2k+2l+2m+2n-(180^{\circ}\times7)[/tex].
Assim, colocando o [tex]2[/tex] em evidência, temos
[tex]2(h+i+j+k+l+m+n)-1260^{\circ}[/tex]
e lembrando que [tex]h+i+j+k+l+m+n[/tex] é a soma total das medidas dos ângulos internos, podemos trocá-la por [tex]900^{\circ}[/tex]. Dessa forma, ficamos com
[tex]2(900^{\circ})-1260^{\circ}=1800^{\circ}-1260^{\circ}=540^{\circ}[/tex].
Em suma, a soma das medidas dos ângulos destacados na figura equivale a [tex]540^{\circ}[/tex].
Solução elaborada pelo COM Grupo Pitagórico, com contribuições dos Moderadores do Blog.