Problema
(Indicado a partir do 1º ano do E. M.)
O proprietário de uma residência instalou, em uma das portas da casa, um alarme formado por dois sensores localizados nos pontos A e B, conforme mostra a figura abaixo. Repare que o ponto A está no batente.
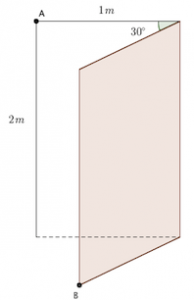
Percebeu-se que o alarme dispara quando a porta aberta forma um ângulo de 30 graus com o batente. Supondo que a porta tem 2 metros de altura e 1 metro de largura, qual a distância entre os sensores que faz o alarme disparar?
Solução
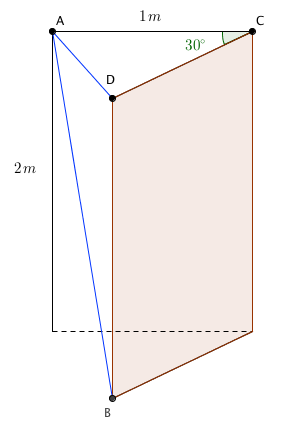
Perceba que [tex]DC = AC = 1m[/tex]; assim, aplicando a lei dos cossenos no [tex]\Delta ACD[/tex], temos
[tex]\qquad AD^2 = 1^2 + 1^2 – 2 \cdot 1 \cdot 1 \cdot cos 30^{\circ}[/tex],
donde
[tex] \qquad AD^2 = 2 – \sqrt{3}[/tex].
Temos [tex]\overline{DB}[/tex] perpendicular ao plano do chão.
Temos também que o plano [tex]ADC[/tex] é paralelo ao plano do chão, então [tex]\overline{DB}[/tex] é perpendicular a ele, o que nos leva a concluir que [tex]A\hat{D}B[/tex] é um ângulo reto.
Aplicando o teorema de Pitágoras no [tex]\Delta ADB[/tex], temos
[tex]\qquad AB^2 = AD^2 + 2^2=2 – \sqrt{3} + 4[/tex],
e, portanto, [tex]\boxed{ AB = \sqrt{6 – \sqrt{3}}}[/tex]
Solução elaborada pelos Moderadores do Blog.
