Problema
(Indicado a partir do 2º ano do E. M.)
Um grande condomínio residencial foi projetado de forma que seis prédios iguais sejam construídos ao longo de uma circunferência de raio [tex]4[/tex] dam, conforme mostra a figura.
Sabe-se ainda que cada prédio visto de cima é um retângulo com lado menor medindo [tex]1[/tex] dam.
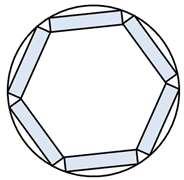
A disposição dos prédios foi projetada de forma que o hexágono interno obtido seja regular e dois vértices de cada retângulo toquem a circunferência.
Calcular o perímetro desse hexágono.
Solução
Observe a figura seguinte, na qual [tex]A[/tex] é o centro da circunferência que delimitará a área onde serão construídos os prédios.
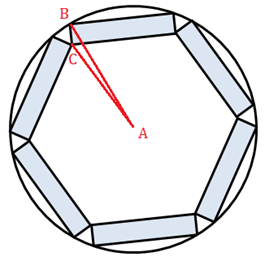
Temos, então,
- [tex]AB=4[/tex] dam;
- [tex]BC=1[/tex] dam;
- [tex]AC=x[/tex] dam.
Assim, [tex]x[/tex] é a medida do lado do hexágono regular (convençam-se disto!).
Observe que a medida do ângulo [tex]\angle{ACB} \, [/tex] é [tex] \, 150^\circ[/tex]; assim, aplicando a Lei dos Cossenos ao triângulo ABC, tem-se:
[tex]\qquad \qquad (AB)^2=(AC)^2+(BC)^2-(AC)(BC)cos(\angle{ACB})[/tex]
donde
[tex]\qquad \qquad 4^2=x^2+1^2-2\cdot x\cdot 1\cdot cos 150^\circ[/tex].
Assim, [tex] x^2+1-2\cdot x\cdot \left(-\dfrac{\sqrt{3}}{2}\right)=16 \, [/tex] e, consequentemente, [tex] x=\dfrac{3\sqrt{7}-\sqrt{3}}{2}[/tex].
Desse modo, o perímetro do hexágono é [tex]6\cdot x=3\left(3\sqrt{7}-\sqrt{3}\right)[/tex] dam.
Solução elaborada pelos Moderadores do Blog.
